



suivant: Développement en série de
monter: Séries de Fourier
précédent: Définition
Table des matières
Soit une série trigonométrique convergente sur
 et de somme
et de somme
 . On montre que :
. On montre que :
et que pour tout  entier supérieur ou égal à
entier supérieur ou égal à 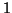 :
On remarquera que grâce à la périodicité, il est possible de
calculer ces intégrales sur tout intervalle
:
On remarquera que grâce à la périodicité, il est possible de
calculer ces intégrales sur tout intervalle
![$ \left[ \alpha,\alpha
+2\pi\right] $](img2026.gif) , où
, où 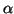 est un réel quelconque.
est un réel quelconque.
Si la fonction  est paire, alors les coefficients
est paire, alors les coefficients 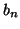 sont tous nuls.
sont tous nuls.
Si la fonction  est impaire, alors les coefficients
est impaire, alors les coefficients 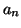 sont tous nuls.
sont tous nuls.
Michel
2002-08-06
![]() et de somme
et de somme
![]() . On montre que :
. On montre que :
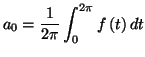
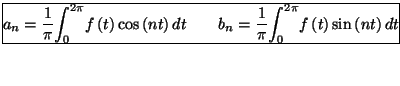
![]() est paire, alors les coefficients
est paire, alors les coefficients ![]() sont tous nuls.
sont tous nuls.
![]() est impaire, alors les coefficients
est impaire, alors les coefficients ![]() sont tous nuls.
sont tous nuls.