Généralités

Définition 8.1   Une équation différentielle est une équation de la forme

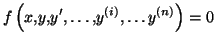$$f\left( x,y,y^{\prime},\ldots,y^{\left( i\right) },\ldots y^{\left( n\right) }\right) =0$$ (E)

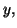
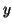
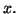
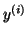
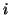
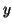
d'inconnue $y,$ où $y$ est une fonction de la variable $x.$ $y^{\left( i\right) }$ représente la dérivée d'ordre $i$ de $y$ par rapport à $x. \index{Equation!différentielle}$

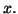
En notation différentielle, on écrit $y^{\left( i\right) } =\frac{d^{i}y}{dx^{i}}.$

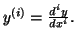
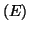
Définition 8.2   Dans l'équation $\left( E\right)$ ci-dessus, $n$ s'appelle l'ordre de l'équation.
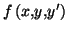
$f\left( x,y,y^{\prime}\right)$ est une équation différentielle du premier ordre .
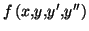
$f\left( x,y,y^{\prime},y^{\prime\prime}\right)$ est une équation différentielle du second ordre.

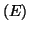
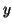
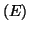
Définition 8.3   Résoudre ou intégrer l'équation différentielle $\left( E\right)$ consiste à trouver toutes les fonctions $y$ qui vérifient l'équation $\left( E\right)$ sur un intervalle $I.$

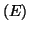
Définition 8.4   Une solution particulière de l'équation différentielle $\left( E\right)$ est une fonction qui vérifie $\left( E\right) . \index{Solution!particulière}$

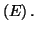
Exercice 8.1   Déterminer une équation différentielle vérifiée par la fonction $f:x\mapsto\cos\left( 2x\right) .$

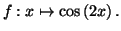
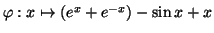
Exercice 8.2   La fonction $\varphi:x\mapsto\left( e^{x}+e^{-x}\right) -\sin x+x$ est-elle une solution sur $\mathbb{R}$ de l'équation diffé rentielle

$$y^{\prime\prime}-y=-x$$