Définition 8.6
Il s'agit d'équations qui s'écrivent après réduction, sous la
forme standard:
où
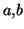
et
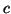
sont des fonctions de la variable réelle
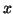
,
continues sur un intervalle
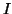
de

sur lequel la fonction
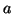
ne
s'annule pas, et
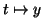
une fonction inconnue à déterminer,
dérivable sur l'intervalle