



suivant: Fractions rationnelles
monter: Arithmétique dans
précédent: Polynômes premiers entre eux
Table des matières
Définition 1.18
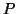
est
irréductible dans
![$ \mathbb{K}\left[ X\right] $](img14.gif)
si
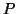
n'est pas constant et si ses seuls diviseurs sont les polynômes constants
et les polynômes
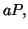
avec
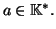
Théorème 1.7 (
de d'Alembert)
Dans
![$ \mathbb{C}\left[ X\right] ,$](img101.gif)
les seuls
polynômes irréductibles sont ceux de degré
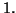
Dans
![$ \mathbb{R}\left[ X\right] ,$](img103.gif)
les seuls polynômes irréductibles sont
ceux de degré
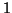
et ceux de degré
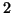
dont le discriminant est
strictement négatif.
Théorème 1.8
Tout polynôme de
![$ \mathbb{K}\left[ X\right] $](img14.gif)
s'écrit de manière
unique sous la forme :
avec
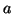
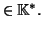
Les
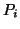
étant des polynômes
irréductibles, unitaires et tous distincts. Les
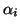
sont des
entiers non nules et

est un certain entier qui dépend du polynôme.
Définition 1.19
Un polynôme est
scindé si tous ses facteurs irréductibles
sont de degré au plus égaux à
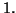
Proposition 1.6
Si
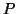
est un polynôme scindé de degré
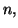
et si
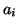
est
racine d'ordre
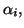
alors
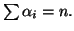
On peut en déduire qu'un polynôme de degré  a exactement
a exactement  racines dans
racines dans
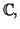 en comptant chaque racine avec son ordre de
multiplicité.
en comptant chaque racine avec son ordre de
multiplicité.
Exercice 1.12
Soit
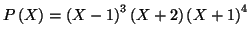
et
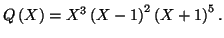
Déterminer un PGCD et un PPCM de
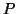
et de
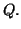
Exercice 1.13
On admet que si
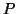
et
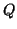
sont deux polynômes et
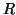
le reste de la
division de
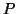
par
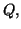
alors
A l'aide de cet algorithme, déterminer le PGCD de
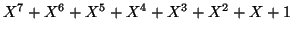
et de
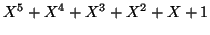




suivant: Fractions rationnelles
monter: Arithmétique dans
précédent: Polynômes premiers entre eux
Table des matières
Michel
2002-08-06
![]() a exactement
a exactement ![]() racines dans
racines dans
![]() en comptant chaque racine avec son ordre de
multiplicité.
en comptant chaque racine avec son ordre de
multiplicité.