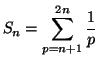suivant: Développements limités
monter: Les outils de l'analyse
précédent: Les outils de l'analyse
Table des matières
Théorème 4.1
Soit

une fonction continue sur
![$ \left[ a,b\right] $](img1026.gif)
et dérivable sur
![$ \left] a,b\right[ .$](img285.gif)
Il existe un réel
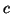
élément de
![$ \left]
a,b\right[ $](img1027.gif)
tel que
Démonstration : On considère la fonction affine 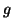 qui
coïncide avec la fonction
qui
coïncide avec la fonction  aux points
aux points  et
et 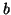 :
:
Il suffit maintenant d'appliquer le théorème de Rolle à la
fonction
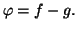
Théorème 4.2
( de Rolle )
Soit

une fonction continue sur le segment
![$ [a,b] $](img1031.gif)
, dérivable sur
![$ ]a,b[
$](img1032.gif)
et telle que
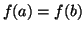
. Il existe alors un réel
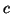
de
![$ ]a,b[
$](img1032.gif)
tel que
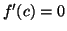
On a :
En utilisant le théorème des accroissements finis, on prouve les deux
théorèmes suivants :
Théorème 4.3
Si

est une fonction dérivable sur un intervalle
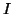
telle que
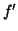
soit positive sur
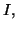
alors

est une fonction croissante sur
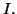
Théorème 4.4
( Inégalité des accroissements finis ) Soit

une fonction
dérivable sur un intervalle
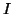
telle qu'il existe deux réels
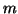
et
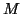
vérifiant :
Alors, pour tout

et
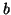
de
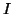
tels que
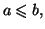
on a
Théorème 4.5
Soit

une fonction dérivable sur un intervalle
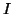
telle qu'il existe
un réel
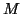
vérifiant :
Alors, pour tout

et
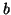
de
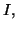
on a
Le théorème des accroissements finis permet d'effectuer le
prolongement de fonctions dérivables selon la propriété :
Proposition 4.1
Soit

une fonction continue sur
![$ \left[ a,b\right] $](img1026.gif)
et dérivable sur
![$ \left] a,b\right[ .$](img285.gif)
Si
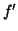
admet en

une limite finie
égale à
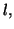
alors

est dérivable en
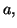
et
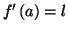
Proposition 4.2
Soit

une fonction continue sur
![$ \left[ a,b\right] $](img1026.gif)
et dérivable sur
![$ \left] a,b\right[ .$](img285.gif)
Si
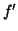
admet en

une limite finie
égale à
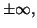
alors

n'est pas dérivable en

Par
contre, la courbe représentative de

admet au point d'abscisse

une
demi-tangente verticale.
Démonstration : On introduit la fonction
![$ \psi:\left[ a,b\right]
\rightarrow\mathbb{R}$](img1044.gif) définie par
définie par
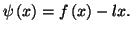 Cette fonction est continue sur
Cette fonction est continue sur
![$ \left[ a,b\right] $](img1026.gif) et
dérivable sur
et
dérivable sur
![$ \left] a,b\right[ .$](img285.gif) On applique le théorème des
accroissements finis à la fonction
On applique le théorème des
accroissements finis à la fonction  sur l'intervalle
sur l'intervalle
![$ \left[
a,x\right] ,$](img1046.gif) pour tout
pour tout  de
de
![$ \left] a,b\right[ .$](img285.gif) Il existe donc un
réel
Il existe donc un
réel
![$ c\in\left] a,x\right[ $](img1047.gif) tel que
tel que
Or, comme 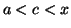 et que
et que
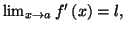 on a donc
on a donc
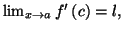 d'où
d'où
Exercice 4.1
Soit

la fonction définie sur
![$ \left] -\pi,\pi\right[ -\left\{
0\right\} $](img1056.gif)
par
Montrer que la fonction

se prolonge par continuité sur
![$ \left]
-\pi,\pi\right[ ,$](img1058.gif)
et que la fonction obtenue est de plus dérivable sur
![$ \left] -\pi,\pi\right[ .$](img1059.gif)
On rappelle les égalités
:
Exercice 4.2
En utilisant le théorème des accroissements finis, démontrer que
pour tout

de

on a
Exercice 4.3
On définit la suite
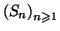
par
-
Etablir l'encadrement suivant :
- En déduire la limite de la suite
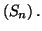
Définition 4.1
Une fonction

définie sur un intervalle
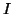
est dite
lipschitzienne de rapport
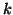
si pour tout

et
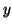
de
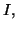
on a :
Exercice 4.4
Soit
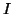
un intervalle de
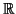
et
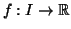
une
application dérivable, à dérivée bornée sur
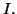
Montrer
que

est lipschitzienne.
Exercice 4.5
Montrer que la fonction
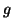
définie sur
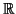
par
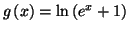
est lipschitzienne de rapport
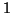
sur
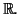




suivant: Développements limités
monter: Les outils de l'analyse
précédent: Les outils de l'analyse
Table des matières
Michel
2002-08-06
![]() qui
coïncide avec la fonction
qui
coïncide avec la fonction ![]() aux points
aux points ![]() et
et ![]() :
:
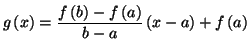
![]() définie par
définie par
![]() Cette fonction est continue sur
Cette fonction est continue sur
![]() et
dérivable sur
et
dérivable sur
![]() On applique le théorème des
accroissements finis à la fonction
On applique le théorème des
accroissements finis à la fonction ![]() sur l'intervalle
sur l'intervalle
![]() pour tout
pour tout ![]() de
de
![]() Il existe donc un
réel
Il existe donc un
réel
![]() tel que
tel que
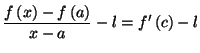

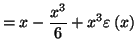 avec
avec 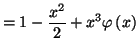 avec
avec