suivant: Génération de développements limités
monter: Les outils de l'analyse
précédent: Le theorème des accroissements
Table des matières
Si  est une fonction définie au voisinage de
est une fonction définie au voisinage de 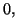 chercher un
développement limité d'ordre
chercher un
développement limité d'ordre  de
de  en 0 consiste à trouver,
s'il existe, un polynôme de degré
en 0 consiste à trouver,
s'il existe, un polynôme de degré  dont la courbe repré
sentative va être une '' bonne '' approximation de la courbe
représentative de
dont la courbe repré
sentative va être une '' bonne '' approximation de la courbe
représentative de 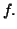 Par exemple, on considère la fonction
Par exemple, on considère la fonction 
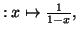 dont la courbe est appelée C, et les fonctions
dont la courbe est appelée C, et les fonctions
dont les courbes représentatives sont notées C1, C2 et C3. On remarque
graphiquement que C3 est une meilleure approximation de la courbe C que ne le
sont C1 et C2.
Définition 4.2
Soit

une fonction définie sur un voisinage de
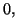
et

un entier
naturel. On dit que

admet un
développement limité à
l'ordre  au voisinage de
au voisinage de 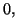
s'il existe un polynôme
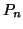
de degré inférieur ou égal à

tel que :
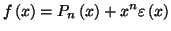
avec
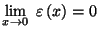
Dans ce cas, on utilise la notation :
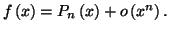
Définition 4.3
Dans ce cas, l'égalité
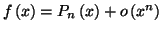
s'appelle le développement limité de

en
0 à l'ordre
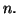
Proposition 4.3
Si une fonction admet un développement limité à l'ordre
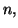
alors
ce développement est unique.
Proposition 4.4
Si

est une fonction paire admettant un développement limité en
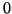
à l'ordre

, alors les coefficients d'ordre impair de son
développement limité sont nuls.
Proposition 4.5
Si

est une fonction impaire admettant un développement limité en
0 à l'ordre

, alors les coefficients d'ordre pair de son
développement limité sont nuls.
Définition 4.4
Si une fonction admet un développement limité en 0 à l'ordre

qui s'écrit
alors
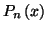
s'appelle la
partie ré
gulière
ou polynomiale du développement, et
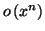
est le reste ou la
partie complémentaire de ce
développement.
Exercice 4.6
On se propose dans cet exercice de déterminer le développement
limité à l'ordre

en 0 de la fonction
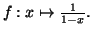
- Etablir pour tout
 de
de
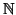 l'égalité :
l'égalité :
- En déduire le développement limité cherché.




suivant: Génération de développements limités
monter: Les outils de l'analyse
précédent: Le theorème des accroissements
Table des matières
Michel
2002-08-06
![]() est une fonction définie au voisinage de
est une fonction définie au voisinage de ![]() chercher un
développement limité d'ordre
chercher un
développement limité d'ordre ![]() de
de ![]() en 0 consiste à trouver,
s'il existe, un polynôme de degré
en 0 consiste à trouver,
s'il existe, un polynôme de degré ![]() dont la courbe repré
sentative va être une '' bonne '' approximation de la courbe
représentative de
dont la courbe repré
sentative va être une '' bonne '' approximation de la courbe
représentative de ![]() Par exemple, on considère la fonction
Par exemple, on considère la fonction ![]()
![]() dont la courbe est appelée C, et les fonctions
dont la courbe est appelée C, et les fonctions
![\includegraphics[scale=0.6]{fig17.eps}](img1078.gif)