



suivant: Fonction polynôme
monter: Polynômes
précédent: Polynômes
Table des matières
Définition 1.1
On désigne par
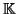
l'ensemble

ou l'ensemble
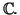
Un
polynôme à coefficients dans
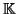
est une suite d'éléments de
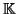
tous nuls à partir d'un
certain rang. C'est donc une suite
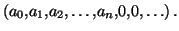
Définition 1.2
Le polynôme
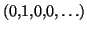
se note
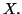
Définition 1.3
L'ensemble des polynômes à coefficients dans
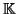
se note
![$ \mathbb{K}\left[ X\right] .$](img10.gif)
Définition 1.4
L'ensemble des polynômes à coefficients dans
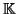
de degré
inférieur ou égal à

(

entier positif strictement ) se note
![$ \mathbb{K}_{n}\left[ X\right] .$](img12.gif)
Définition 1.5
On désigne par
![$ \mathbb{K}_{n}\left[ X\right] $](img13.gif)
l'ensemble des
polynômes de
![$ \mathbb{K}\left[ X\right] $](img14.gif)
dont le degré est
inférieur ou égal à
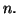
Proposition 1.1
![$ \left( \mathbb{K}\left[ X\right] ,+,\;.\;\right) $](img16.gif)
est un espace
vectoriel sur
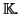
( Le point désigne la multiplication par un
élément de
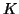
)
Proposition 1.2
Tout élément de
![$ \mathbb{K}\left[ X\right] $](img14.gif)
s'écrit de
manière unique sous la forme
Définition 1.6
On appelle
degré d'un polynôme l'indice du dernier
coefficient non nul dans la suite des coefficients.
On a pour tout 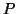 et
et 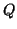 éléments de
éléments de
![$ \mathbb{K}\left[ X\right] $](img14.gif) :
:
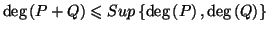
et
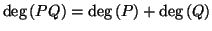
Définition 1.7
Le polynôme
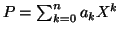
est dit
unitaire si
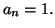
Définition 1.8
Si
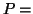
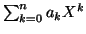
désigne un élément de
![$ \mathbb{K}\left[ X\right] ,$](img28.gif)
alors le
polynôme dérivé
de
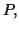
noté
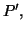
est par définition égal à
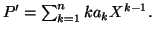




suivant: Fonction polynôme
monter: Polynômes
précédent: Polynômes
Table des matières
Michel
2002-08-06
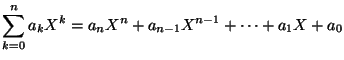
![]() et
et ![]() éléments de
éléments de
![]() :
: