



suivant: Utilisation de développements limités
monter: Les outils de l'analyse
précédent: Génération de développements limités
Table des matières
Théorème 4.6
Soit

une fonction de classe
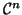
( c'est à dire
dérivable

fois et dont la dérivée n-ième est continue )
sur un intervalle de la forme
![$ \left] -\alpha,\alpha\right[ ,$](img1113.gif)
avec
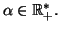
Alors

admet un développement limité
à l'ordre

au voisinage de 0 qui est donné par la formule
suivante, appelée de
Taylor-Young :
A l'aide de cette formule, on peut établir les développements
limités des fonctions usuelles, qui sont donnés par :
Exercice 4.10
Déterminer les développements limités à l'ordre

au
voisinage de 0 des fonctions cosinus hyperbolique et sinus hyperbolique.
Exercice 4.11
Déterminer le développement limité à l'ordre

au voisinage
de 0 de la fonction
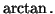
Exercice 4.12
Déterminer le développement limité à l'ordre
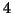
au voisinage
de 0 de
Exercice 4.13
Déterminer le développement limité à l'ordre
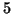
au voisinage
de 0 de
Exercice 4.14
Déterminer le développement limité à l'ordre
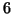
au voisinage
de 0 de
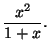
En déduire celui de
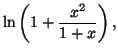
toujours à l'ordre
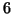
et au voisinage de




suivant: Utilisation de développements limités
monter: Les outils de l'analyse
précédent: Génération de développements limités
Table des matières
Michel
2002-08-06
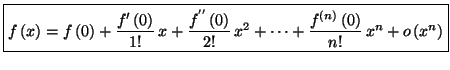
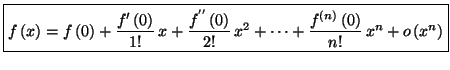
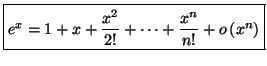
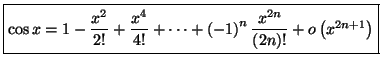
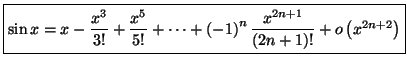
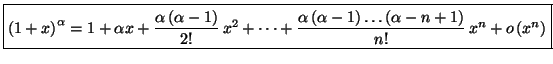
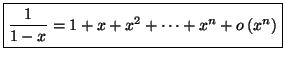
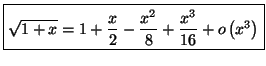
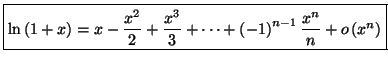
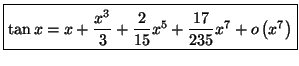
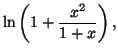 toujours à l'ordre
toujours à l'ordre