Théorème 4.7
Soient
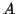
et
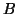
deux polynômes à coeffficients réels tels que
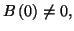
et

un entier. Il existe un couple unique de
polynômes
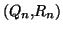
tels que
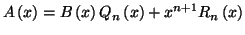
avec
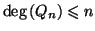
Pratiquement, effectuons la division selon les puissances croissantes du
polynôme 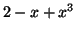 par le polynôme
par le polynôme
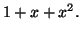
![]() par le polynôme
par le polynôme
![]()
![$\displaystyle \begin{tabular}[c]{ccccccc\vert ccccc}
$2$\ & $-x$\ & & $+x^{3}$\...
...& & & & & \\ \cline{5-7}
& & & & & $x^{5}$\ & $4x^{6}$\ & & & & &
\end{tabular}$](img1141.gif)