



suivant: Intégration par parties
monter: Méthodes de calcul des
précédent: Méthodes de calcul des
Table des matières
Si  est une fonction continue sur
est une fonction continue sur
![$ \left[ a,b\right] ,$](img1284.gif) alors elle admet
des primitives sur
alors elle admet
des primitives sur
![$ \left[
a,b\right] .$](img282.gif) Lorsque l'on peut en calculer une,
cela fournit la valeur de
Lorsque l'on peut en calculer une,
cela fournit la valeur de
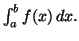
Définition 5.3
La notation
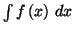
désigne une primitive de la
fonction
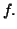
Les primitives usuelles sont données dans le tableau suivant
:
On rappelle les relations suivantes :
Exercice 5.8
Calculer les intégrales suivantes :
Exercice 5.9
En utilisant une décomposition en éléments simples, calculer
l'intégrale suivante :
Exercice 5.10
On définit les intégrales suivantes
Calculer
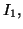
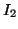
et en déduire la valeur de
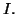
Michel
2002-08-06
![]() est une fonction continue sur
est une fonction continue sur
![]() alors elle admet
des primitives sur
alors elle admet
des primitives sur
![]() Lorsque l'on peut en calculer une,
cela fournit la valeur de
Lorsque l'on peut en calculer une,
cela fournit la valeur de
![]()
![\begin{displaymath}
\begin{tabular}[c]{\vert c\vert c\vert c\vert c\vert}\hline\...
...dx=x\ln x-x+C$\ &
$\mathbb{{R}_{+}^{*}}$\\ \hline
\end{tabular}\end{displaymath}](img1331.gif)
![$\displaystyle =\frac12\ln\left\vert \frac{1+x}{1-x}\right\vert \,\forall x\in\m...
...me*{Arccos} x+\operatorname*{Arcsin}x=\frac\pi2\,\forall x\in\left] -1,1\right[$](img1335.gif)