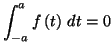suivant: Calcul approché des intégrales
monter: Méthodes de calcul des
précédent: Intégration par parties
Table des matières
Théorème 5.9
Soient
et
des intervalles de
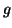
une application de
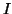
dans
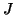
de classe
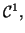
et

une fonction appartenant à
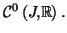
Pour tout
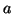
et
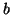
de
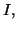
on a
Soit 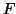 une primitive de
une primitive de  sur
sur 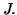 On a de manière évidente
On a de manière évidente
Comme
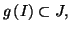 on a
on a
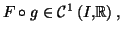 et
et
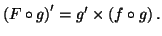 On en déduit que
On en déduit que
Exemple : Calculons 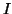 =
=
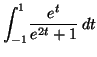 .
.
On pose 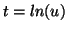
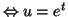 . On en déduit que
. On en déduit que
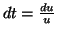 .
.
Pour 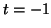 ,
, 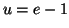 et pour
et pour 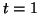 ,
, 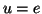 . D'où
. D'où
On n'oubliera pas de changer les bornes d'intégration.
Exercice 5.13
A l'aide du changement de variable défini par
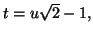
calculer
l'intégrale
Exercice 5.14
En posant
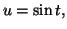
calculer l'intégrale

Exercice 5.15
Calculer l'intégrale
à l'aide du changement de variable défini par
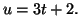
Exercice 5.16
Soit

une fonction continue et paire sur l'intervalle
![$ \left[ -a,a\right]
.$](img1374.gif)
Etablir à l'aide du changement de variable défini par
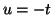
que
On peut de même démontrer que si  est impaire, on a alors :
est impaire, on a alors :




suivant: Calcul approché des intégrales
monter: Méthodes de calcul des
précédent: Intégration par parties
Table des matières
Michel
2002-08-06
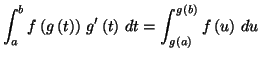
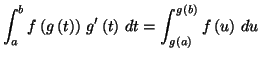
![]() une primitive de
une primitive de ![]() sur
sur ![]() On a de manière évidente
On a de manière évidente
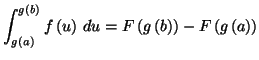
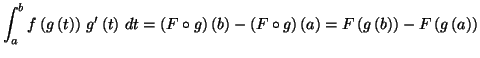
![]() =
=
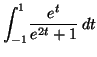 .
.
![]()
![]() . On en déduit que
. On en déduit que
![]() .
.
![]() ,
, ![]() et pour
et pour ![]() ,
, ![]() . D'où
. D'où
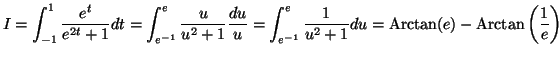
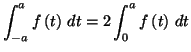
![]() est impaire, on a alors :
est impaire, on a alors :