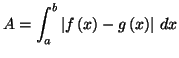suivant: Méthode des rectangles
monter: Calcul approché des intégrales
précédent: Calcul approché des intégrales
Table des matières
Le plan est rapporté à un repère
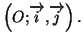
Proposition 5.4
Si

est une fonction continue et positive sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
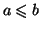
, ( voir la figure 1 ) alors l'aire du domaine plan limité
par la courbe représentative de
l'axe des abscisses, les droites
d'équation
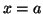
et
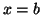
est égale à
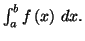
On prendra garde que le résultat obtenu est en unité d'aire, et
qu'il faudra le multiplier par l'unité choisie pour le graphique. En
abrégé, l'unité d'aire se note 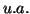
Pour une fonction  à valeurs négatives sur
à valeurs négatives sur
![$ \left[ a,b\right] ,$](img1284.gif) l'aire entre la courbe, l'axe des abscisses et les droites d'équation
l'aire entre la courbe, l'axe des abscisses et les droites d'équation
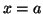 et
et 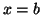 est donnée par
est donnée par
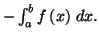
Lorsque la fonction  n'est pas de signe constant, comme dans le cas de la
figure 2, on obtient pour l'aire hachurée la valeur
n'est pas de signe constant, comme dans le cas de la
figure 2, on obtient pour l'aire hachurée la valeur
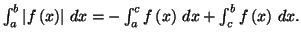
Proposition 5.5
Si

et
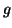
sont deux fonctions continues sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
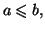
alors l'aire comprise entre les courbes d'équation
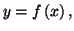
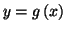
et les droites d'équation
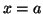
et
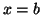
est donnée par :
Il suffit alors de connaître la position respective des courbes pour
calculer cette intégrale.
Exercice 5.17
Déterminer l'aire délimitée par les droites d'équations
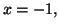
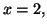
et par les courbes d'équations
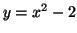
et
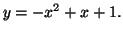




suivant: Méthode des rectangles
monter: Calcul approché des intégrales
précédent: Calcul approché des intégrales
Table des matières
Michel
2002-08-06
![]()
![]()
![\includegraphics[]{fig21.eps}](img1381.gif)
![]() à valeurs négatives sur
à valeurs négatives sur
![]() l'aire entre la courbe, l'axe des abscisses et les droites d'équation
l'aire entre la courbe, l'axe des abscisses et les droites d'équation
![]() et
et ![]() est donnée par
est donnée par
![]()
![]() n'est pas de signe constant, comme dans le cas de la
figure 2, on obtient pour l'aire hachurée la valeur
n'est pas de signe constant, comme dans le cas de la
figure 2, on obtient pour l'aire hachurée la valeur
![]()