Méthode des rectangles

Soit $f$ une fonction numérique monotone sur $\left[ a,b\right] ,$ avec $a\leqslant b$ . Supposons par exemple que $f$ est croissante. L'entier $n\in\mathbb{N}^{*}$ étant fixé, on pose $h=\frac{b-a}{n},$ et on prend comme subdivision de $\left[ a,b\right]$ la subdivision régulière de pas $h.$ Pour tout $k$ de $\mathbb{N}_{n}^{*},$ on a de manière évidente :

$$hf\left( a+\left( k-1\right) h\right) \leqslant\int_{a+\left( k-1\right) h}^{a+kh}f\left( x\right) \,dx\leqslant hf\left( a+kh\right)$$

Par addition, on obtient l'encadrement

$$h\sum_{k=0}^{n-1}f\left( a+kh\right) \leqslant\int_{a}^{b}f\left( x\right) \,dx\leqslant h\sum_{k=1}^{n}f\left( a+kh\right)$$ (8.3)

Lorsque $f$ est positive, le premier et le dernier terme de l'iné galité (8.3) s'interprètent comme des sommes d'aires de rectangles. Ces sommes fournissent donc une valeur approchée de $\int_{a}^{b}f\left( x\right) \,dx$ avec une erreur au plus égale à

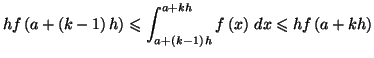
$$h\sum_{k=1}^{n}f\left( a+kh\right) -h\sum_{k=0}^{n-1}f\left( a+kh... ...\frac{\left( b-a\right) \left[ f\left( b\right) -f\left( a\right) \right] }{n}$$

On remarquera que la précision obtenue est de l'ordre de $\frac{1}{n}.$

Exercice 5.18   Le but de cet exercice est d'obtenir une valeur approchée de l'intégrale :

$$I=\int_{1}^{3}\frac{1}{2+x^{3}}dx$$

Soit $f$ la fonction définie sur $\left[ 1,3\right]$ par $f\left( x\right) =\frac{1}{2+x^{3}}$ et $C$ sa courbe représentative.

1. Détermination d'une valeur approchée de $I$ par la méthode des rectangles. On divise l'intervalle $\left[ 1,3\right]$ en dix intervalles de même longueur $0,2$ et on construit les rectangles '' inférieurs '' et les rectangles '' supérieurs ''.
   1. Calculer l'aire totale de la réunion des dix rectangles '' supérieurs ''.

   2. Calculer l'aire totale de la réunion des dix rectangles '' inférieurs ''.

   3. En déduire un encadrement de $I$ et donner une valeur approchée de $I$ avec une incertitude inférieure à $5.10^{-2}.$

2. Détermination d'une valeur approchée de $I$ par la méthode du point milieu ( ou médian ). On utilise la même subdivision en dix intervalles de l'intervalle $\left[ 1,3\right]$ qu'à la question précédente.

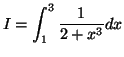
   Les rectangles représentés ci-dessus sont construits en utilisant l'ordonnée du milieu de chaque segment composant la subdivision. Calculer la valeur approchée de $I$ obtenue en ajoutant les aires des dix rectangles.

3. Détermination d'une valeur approchée de $I$ par la méthode des trapèzes. . On utilise toujours la subdivision de $\left[ 1,3\right]$ en dix intervalles de même longueur. Une meilleure valeur approchée de $I$ que celle obtenue à la question précédente semble être obtenue en additionnant les aires des trapèzes obtenus en joignant les points de coordonnées $\left( x_{i},f\left( x_{i}\right) \right)$ et $\left( x_{i+1},f\left( x_{i+1}\right) \right)$ pour $i$ variant de $1$ à $10.$ Déterminer ainsi une nouvelle valeur approchée de $I.$