



suivant: Calcul des intégrales impropres
monter: Intégrales généralisées
précédent: Intégrales généralisées
Table des matières
On désignera dans la suite de ce chapître par 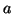 un réel et par
un réel et par
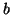 un élément de
un élément de
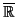 tels que
tels que 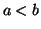 .
.
Définition 5.7
On dit que la fonction numérique

définie sur un intervalle
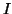
est
localement intégrable
sur
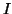
si pour tout intervalle fermé borné
![$ \left[ u,v\right] $](img1463.gif)
inclus dans
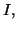
la restriction de

à
![$ \left[ u,v\right] $](img1463.gif)
est intégrable sur
![$ \left[ u,v\right] .$](img1464.gif)
Définition 5.8
Si

est une fonction localement intégrable sur
![$ \left[ a,b\right] ,$](img1284.gif)
alors on dit que l'intégrale de
 converge
converge
sur
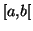
si l'application
admet une limite
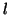
quand
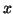
tend vers
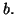
Dans ce cas,
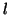
s'appelle
l'intégrale impropre ou
généralisée
de

sur
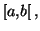
que l'on note
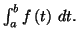
Définition 5.9
Dans le cas contraire, on dit que l'intégrale de

est
divergente
sur
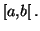
On peut de même définir l'intégrale généralisée de  sur
sur
![$ \left] c,a\right] ,$](img1469.gif) avec
avec
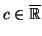 et
et
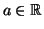 tels que
tels que 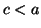 comme la limite quand
comme la limite quand 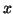 tend vers
tend vers 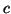 ,
lorsqu'elle existe, de
,
lorsqu'elle existe, de
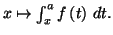
Exercice 5.23
Etudier la convergence ou la divergence des intégrales
:




suivant: Calcul des intégrales impropres
monter: Intégrales généralisées
précédent: Intégrales généralisées
Table des matières
Michel
2002-08-06
![]() un réel et par
un réel et par
![]() un élément de
un élément de
![]() tels que
tels que ![]() .
.
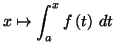
![]() sur
sur
![]() avec
avec
![]() et
et
![]() tels que
tels que ![]() comme la limite quand
comme la limite quand ![]() tend vers
tend vers ![]() ,
lorsqu'elle existe, de
,
lorsqu'elle existe, de
![]()