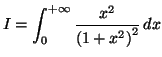Soit ![]() une fonction localement intégrable sur
une fonction localement intégrable sur
![]() On
suppose que l'intégrale de
On
suppose que l'intégrale de ![]() sur
sur
![]() est convergente.
Pour calculer cette intégrale, on effectuera un calcul classique de
l'intégrale de
est convergente.
Pour calculer cette intégrale, on effectuera un calcul classique de
l'intégrale de ![]() sur
sur
![]() , par recherche de
primitives, par intégration par parties, ou par changement de variable,
puis on fera tendre
, par recherche de
primitives, par intégration par parties, ou par changement de variable,
puis on fera tendre ![]() vers
vers ![]() pour obtenir la valeur de
pour obtenir la valeur de
![]()