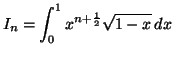 |
- Soient
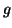 et
et 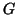 les fonctions définies sur
les fonctions définies sur
![$ \left[ 0,1\right] $](img1318.gif) par :
par :
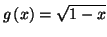 et
et 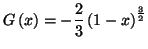
Vérifier que G est la primitive de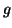 qui s'annule en 1.
qui s'annule en 1.
- Pour tout entier
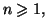 établir à l'aide d'une intégration par parties que :
établir à l'aide d'une intégration par parties que :
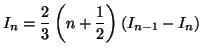
On remarquera que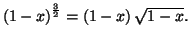
- En déduire l'expression de
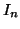 en fonction de
en fonction de 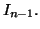
- En admettant que
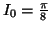 , calculer alors les valeurs
de
, calculer alors les valeurs
de 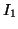 et
et 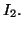
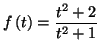 et
et ![$ \varphi ^{\prime }\left( x\right) =\dfrac{%%
-4\left( x+1\right) }{\left[ \left( x+2\right) ^{2}+1\right] \left[ x^{2}+1\right] }$](img1498.gif) pour tout
pour tout