Solution 5.1 : On trouve :
![]()
![]()
![]() et
et ![]()
Solution 5.2 : On écrit en utilisant la
relation de Chasles :
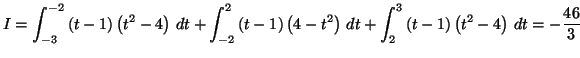
Solution 5.3 :

Solution 5.4 :
![]() .
.
Solution 5.5 : 1) Comme pour tout ![]() de
de
![]()
![]() on en déduit que
on en déduit que
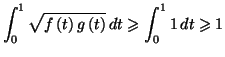
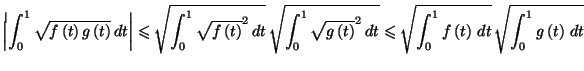
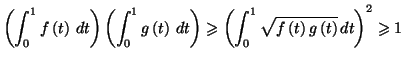
Solution 5.7 : La fonction
![]() est continue sur
est continue sur
![]() donc
donc
![]() est
dérivable sur
est
dérivable sur
![]() de dérivée
de dérivée
![]() Par
dérivation du produit, on a :
Par
dérivation du produit, on a :
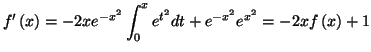
Solution 5.8 : On obtient les résultats
suivants :
![$\displaystyle I_{1}=\int_{1}^{e}\frac{\ln t}{t}\,dt=\int_{1}^{e}\frac{\ln t}{t}\,dt=\left[
\frac{1}{2}\ln^{2}t\right] _{1}^{e}=\frac{1}{2}
$](img1523.gif)
![$\displaystyle I_{2}=\int_{0}^{1}\left( 1-x\right) \sqrt{x}\,dx=\left[ \frac{2}{3}
x^{\frac{3}{2}}-\frac{2}{5}x^{\frac{5}{2}}\right] _{0}^{1}=\frac{4}{15}
$](img1524.gif)
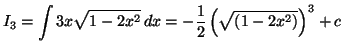
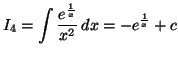
Solution 5.9 : On a :

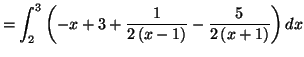 |
||
![$\displaystyle =\left[ -\frac{1}{2}x^{2}+3x+\frac{1}{2}\ln\left( 2x-2\right) -\frac {5}{2}\ln\left( 2x+2\right) \right] _{2}^{3}$](img1530.gif) |
||
![$\displaystyle I_{1}=\left[ \frac{\ln\left( 1+2\sin x\right) }{2}\right] _{0}^{\frac{\pi
}{2}}=\ln\left( \sqrt{3}\right)
$](img1532.gif)
Solution 5.11 : On obtient :
Solution 5.12 : On effectue une première
intégration par parties :
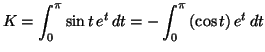 en posant
en posant 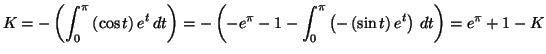
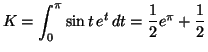
Solution 5.13 : On a
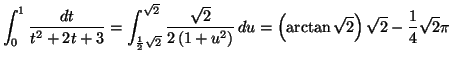
Solution 5.14 : On a :

Solution 5.15 : On a ![]() d'où
d'où
![]()
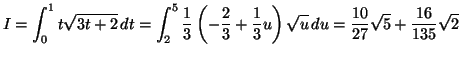
Solution 5.17 : On commence par étudier les
positions respectives des deux courbes sur
![]() On trouve
que :
On trouve
que :
![\includegraphics[scale=0.6]{fig24.ps}](img1546.gif)
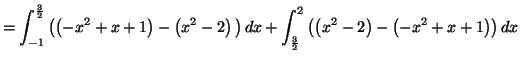 |
||
 |
||
Solution 5.18 : On obtient les résultats
suivants :
(1) (a)
![]()
(1) (b)
![]()
(1) (c) On en déduit que
![]() et on peut proposer
et on peut proposer
![]()
(2)
![]()
(3) En utilisant
l'aire d'un trapèze,il vient :
![$\displaystyle =\left[ \frac{\left( f\left( 1\right) +f\left( 1,2\right) \right)...
...\frac{\left( f\left( 2,8\right) +f\left( 3\right) \right) \times0,2} {2}\right]$](img1563.gif) |
||
Solution 5.19 : On reconnaît une somme de
Riemann, d'où
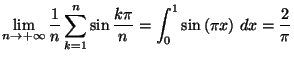
Solution 5.20 : On reconnaît une somme de
Riemann
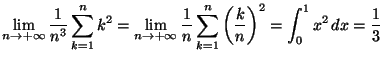
Solution 5.21 : En calculant le logarithme
népérien de cette expression strictement positive, on trouve que :
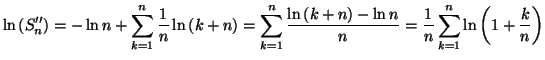
![$\displaystyle \ln S=\int_{0}^{1}\ln\left( 1+x\right) dx=\left[ \left( x+1\right)
\ln\left( x+1\right) -x\right] _{0}^{1}=2\ln2-1
$](img1568.gif)
Solution 5.22 : 1) Evident.
2)
![]()
![]() On peut utiliser soit la formule donnant le
volume d'un cône de révolution
On peut utiliser soit la formule donnant le
volume d'un cône de révolution
![]() ou
montrer qu'une équation de la droite
ou
montrer qu'une équation de la droite
![]() est
est
![]() et en déduire que le volume cherché est donné
par la formule :
et en déduire que le volume cherché est donné
par la formule :

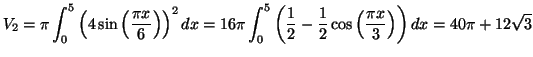
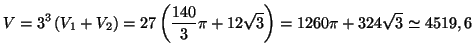 cm
cm
Solution 5.23 : On obtient les résultats
suivants :
![]() donc l'intégrale est convergente, et
donc l'intégrale est convergente, et
![]()
![]() Or
Or
![]() , donc l'intégrale est
divergente.
, donc l'intégrale est
divergente.
![]() donc l'intégrale est convergente, et
donc l'intégrale est convergente, et
![]()
![]() donc
l'intégrale est divergente.
donc
l'intégrale est divergente.
![]() donc l'intégrale est divergente.
donc l'intégrale est divergente.
Solution 5.24 : On effectue une intégration
par parties sur
![]() d'où
d'où
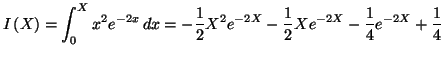
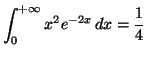
Solution 5.25 : On effectue le changement de
variable proposé, mais pour l'intégrale définie suivante :
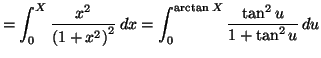 |
||
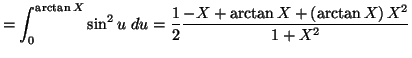 |
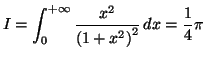
Solution 5.26 :
1. Il suffit de vérifier que
![]() et que pour tout
et que pour tout ![]() de
de
![]() on a
on a
![]()
2. On effectue une intégration par parties :
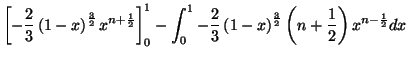 |
|||
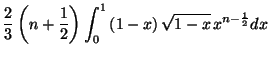 |
|||
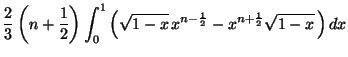 |
|||
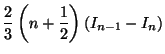 |
Solution 5.27 :
1. ![]() est paire, donc
est paire, donc
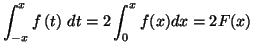
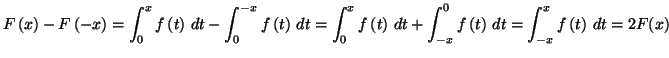 |
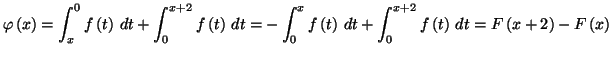 |
![$\displaystyle \varphi ^{\prime }\left( x\right) =f\left( x+2\right) -f\left( x\...
...ft( x+1\right) }{\left[ \left( x+2\right) ^{2}+1\right] \left[ x^{2}+1\right] }$](img1613.gif) |
 |
 |
|
|
0 | ||||
|
|
|||||
|
|
|||||