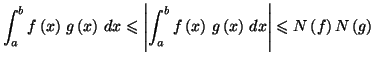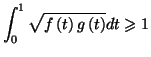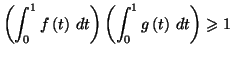suivant: Intégrales et primitives
monter: Intégration
précédent: Linéarité
Table des matières
Théorème 5.1
Soient

et
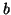
deux réels tels que
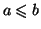
,

désignant
une fonction continue sur
![$ \left[ a,b\right] $](img1026.gif)
telle que
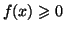
pour tout

de
![$ \left[ a,b\right] $](img1026.gif)
. Alors
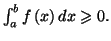
Théorème 5.2
Soient

et
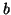
deux réels tels que
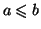
,

et
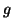
désignant deux fonctions continues sur
![$ \left[ a,b\right] $](img1026.gif)
telles que
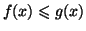
pour tout

de
![$ \left[ a,b\right] $](img1026.gif)
. Alors
On peut appliquer le théorème 5.1 à la
fonction 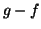 .
.
Il existe un théorème plus précis souvent utile dans la pratique :
Théorème 5.3 (de séparation)
Si

est une fonction continue, de signe constant sur
![$ \left[ a,b\right] ,$](img1284.gif)
alors la condition
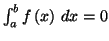
équivaut à

pour tout

de
![$ \left[
a,b\right] .
\index{Théorème@Théorème!de séparation@de séparation}$](img1286.gif)
Théorème 5.4 (Formule de la moyenne)
Soient

et
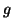
deux fonctions continues sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
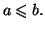
On suppose que la fonction
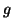
est
positive sur
![$ \left[
a,b\right] .$](img282.gif)
On appelle
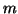
et
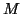
respectivement la
borne inférieure et la borne supérieure de

sur
![$ \left[
a,b\right] .$](img282.gif)
On a
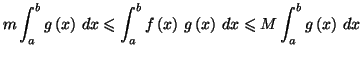 |
(8.1) |
Si de plus la fonction

est continue, alors il existe

![$ \left[ a,b\right] $](img1026.gif)
tel que

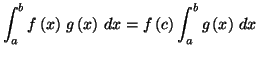 |
(8.2) |
Les inégalités (8.1) résultent immédiatement du fait que pour
tout  de
de
![$ \left[ a,b\right] ,$](img1284.gif) on ait
on ait
Si
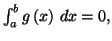 alors d'après (8.1), on a
alors d'après (8.1), on a
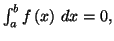 donc la relation (8.2) est vraie pour
tout réel
donc la relation (8.2) est vraie pour
tout réel 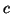 de
de
![$ \left[
a,b\right] .$](img282.gif)
Si
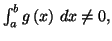 alors le nombre
alors le nombre 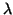 défini par
défini par
 vérifie
vérifie
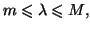 et la propriété (8.2) découle des
théorèmes de continuité.
et la propriété (8.2) découle des
théorèmes de continuité.
Proposition 5.3
Soit

une fonction continue sur
![$ \left[ a,b\right] $](img1026.gif)
, avec
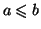
. On a :
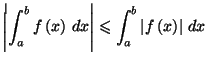 |
(5.1) |
Si l'on ne suppose plus que
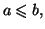 alors on a l'inégalité
plus générale :
alors on a l'inégalité
plus générale :
Définition 5.2
Soit

une fonction continue sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
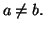
La
valeur moyenne de

sur
![$ \left[ a,b\right] $](img1026.gif)
est le réel
L'interprétation graphique consiste à considérer une fonction  à valeurs positives sur
à valeurs positives sur
![$ \left[
a,b\right] .$](img282.gif) L'aire définie entre
la courbe, l'axe des abscisses et les droites verticales d'équations
L'aire définie entre
la courbe, l'axe des abscisses et les droites verticales d'équations 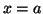 et
et 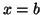 est de même mesure que l'aire du rectangle de dimensions
est de même mesure que l'aire du rectangle de dimensions
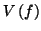 sur
sur
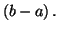
Théorème 5.5 (
Inégalité de Cauchy-Schwarz)
Soient

et
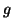
deux
fonctions numériques continues sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
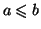
. On a
Il suffit de remarquer que pour tout 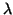 réel, on a
réel, on a
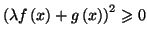 pour tout
pour tout  de
de
![$ \left[ a,b\right] ,$](img1284.gif) et donc
et donc
Ce trinôme en 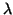 étant toujours positif a un discriminant
négatif ou nul, c'est à dire que
On obtient le résultat demandé par l'application de la racine
carrée.
étant toujours positif a un discriminant
négatif ou nul, c'est à dire que
On obtient le résultat demandé par l'application de la racine
carrée.
Théorème 5.6 (Inégalité de Minkowski)
Soient

et
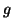
deux fonctions
numériques continues sur
![$ \left[ a,b\right] ,$](img1284.gif)
avec
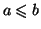
. On a
Si l'on pose pour tout fonction intégrable 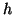 sur
sur
![$ \left[ a,b\right] $](img1026.gif)
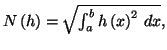 alors on
a en utilisant l'inégalité de Cauchy-Schwarz
alors on
a en utilisant l'inégalité de Cauchy-Schwarz 
On en déduit que
Le passage à la racine carrée fournit alors l'inégalité de Minkowsky.
Exercice 5.4
Déterminer la valeur moyenne de la fonction
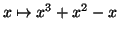
sur
![$ \left[ 1,3\right] .$](img1317.gif)
Exercice 5.5
Soient

et
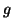
deux fonctions définies sur
![$ \left[ 0,1\right] $](img1318.gif)
à
valeurs dans

continues et positives telles que pour tout

de
![$ \left[
0,1\right] ,$](img902.gif)
on ait
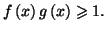
- Démontrer que :
- En appliquant l'inégalité de Cauchy-Schwarz, établir que
- En déduire que :




suivant: Intégrales et primitives
monter: Intégration
précédent: Linéarité
Table des matières
Michel
2002-08-06
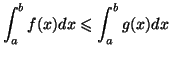
![]() .
.
![]() de
de
![]() on ait
on ait
![]() alors d'après (8.1), on a
alors d'après (8.1), on a
![]() donc la relation (8.2) est vraie pour
tout réel
donc la relation (8.2) est vraie pour
tout réel ![]() de
de
![]()
![]() alors le nombre
alors le nombre ![]() défini par
défini par
![]() vérifie
vérifie
![]() et la propriété (8.2) découle des
théorèmes de continuité.
et la propriété (8.2) découle des
théorèmes de continuité.
![]() alors on a l'inégalité
plus générale :
alors on a l'inégalité
plus générale :

![]() à valeurs positives sur
à valeurs positives sur
![]() L'aire définie entre
la courbe, l'axe des abscisses et les droites verticales d'équations
L'aire définie entre
la courbe, l'axe des abscisses et les droites verticales d'équations ![]() et
et ![]() est de même mesure que l'aire du rectangle de dimensions
est de même mesure que l'aire du rectangle de dimensions
![]() sur
sur
![]()
![\includegraphics[]{fig20.eps}](img1306.gif)
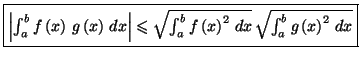
![]() réel, on a
réel, on a
![]() pour tout
pour tout ![]() de
de
![]() et donc
et donc
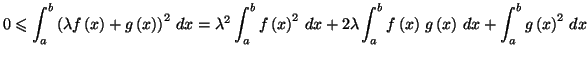
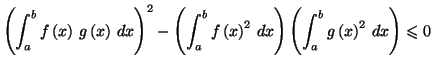
![]() sur
sur
![]()
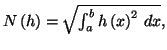 alors on
a en utilisant l'inégalité de Cauchy-Schwarz
alors on
a en utilisant l'inégalité de Cauchy-Schwarz ![]()