![\includegraphics[scale=0.3]{capes10.eps}](img1433.gif)
Le théorème suivant permet de calculer des volumes en utilisant le calcul intégral :
![\includegraphics[scale=0.3]{capes10.eps}](img1433.gif)
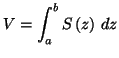
Cette formule se simplifie dans le cas d'un solide de révolution. Prenons
le cas du solide engendré par la rotation autour de l'axe
![]() de la courbe d'équation
de la courbe d'équation
![]() avec
avec
![]() Le volume de ce solide est donné par la formule
suivante :
Le volume de ce solide est donné par la formule
suivante :
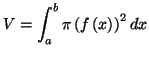
![\includegraphics[scale=0.3]{capes12.eps}](img1456.gif)