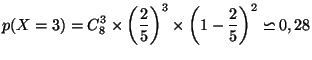Exemple 2

$\;$

Une urne contient 2 boules blanches et 3 noires. On tire au hasard une boule que l'on remet dans l'urne, après avoir noté sa couleur. Soit B l'évènement `` obtenir une blanche `` et N `` obtenir une noire ``. On effectue 8 tirages dans les mêmes conditions. Quelle est la probabilié d'obtenir exactement trois boules blanches ?

Soit $X$ la variable aléatoire égale au nombre de boules blanches obtenues après les 8 tirages. $X$suit la loi binomiale de paramètres 8 et $p=p(B)=\frac{2}{5}$, donc

$$p(X=3)=C_{8}^{3}\times \left(\frac{2}{5}\right)^{3}\times \left(1-\frac{2}{5}\right)^{2}\backsimeq 0,28$$

On a de manière évidente $\overline{X}=\frac{16}{5}$ et $\sigma (X)=\sqrt{8\times \frac{2}{5}\times (1-\frac{2}{5})}\backsimeq 1,38$