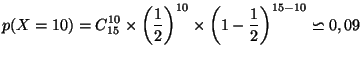![]()
On lance une pièce de monnaie bien équilibrée. Quelle est la probabilité d'obtenir 10 piles en 15 lancers ?
On appelle ![]() le nombre de piles obtenus en 15 lancers.
le nombre de piles obtenus en 15 lancers. ![]() suit
une loi binomiale, car l'expérience consiste en la réalisation de
15 épreuves élémentaires n'ayant que deux issues possibles, chaque
épreuve étant indépendante. Le paramètre
suit
une loi binomiale, car l'expérience consiste en la réalisation de
15 épreuves élémentaires n'ayant que deux issues possibles, chaque
épreuve étant indépendante. Le paramètre ![]() de cette loi vaut 15,
tandis que
de cette loi vaut 15,
tandis que ![]() est égal à la probabilité d'obtenir pile lors d'un
lancer, c'est à dire
est égal à la probabilité d'obtenir pile lors d'un
lancer, c'est à dire
![]() .
. ![]() suit donc la loi binomiale
suit donc la loi binomiale
![]() , et la probabilité d'obtenir 10 piles
en 15 lancers est égale à
, et la probabilité d'obtenir 10 piles
en 15 lancers est égale à