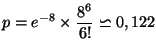


suivant: Loi normale
monter: Loi de Poisson
précédent: Exemple
Table des matières
Théorème 2
On admet que si
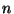
est grand,
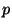
voisin de 0 et
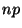
pas trop
grand, alors la loi
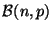
est très proche de la loi
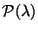
, où
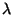
=np.
Dans une entreprise, on considère que la probabilité d'obtenir un
article défectueux à la sortie d'une chaine de fabrication est 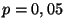 .
Lors d'un contrôle de qualité, on envisage de prélever un échantillon
de 120 articles. Bien que ce prélèvement soit exhaustif, nous considérons
que la production est suffisamment importante pour qu'on puisse assimiler
ce prélèvement à 120 tirages avec remise, donc indépendants, d'un
article défectueux ou non. La variable aléatoire
.
Lors d'un contrôle de qualité, on envisage de prélever un échantillon
de 120 articles. Bien que ce prélèvement soit exhaustif, nous considérons
que la production est suffisamment importante pour qu'on puisse assimiler
ce prélèvement à 120 tirages avec remise, donc indépendants, d'un
article défectueux ou non. La variable aléatoire  mesurant le
nombre d'articles défectueux d'un tel échantillon suit la loi binomiale
mesurant le
nombre d'articles défectueux d'un tel échantillon suit la loi binomiale
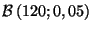 , et l'espérance mathématique de
, et l'espérance mathématique de
 est
est
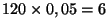 . Comparons la loi de
. Comparons la loi de  avec celle
d'une variable aléatoire
avec celle
d'une variable aléatoire 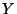 suivant la loi de Poisson
suivant la loi de Poisson
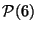 .
.
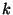 |
Loi de  |
Loi de 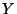 |
| 0 |
0,002 |
0,002 |
| 1 |
0,013 |
0,015 |
| 2 |
0,042 |
0,045 |
| 3 |
0,087 |
0,089 |
| 4 |
0,134 |
0,134 |
| 5 |
0,163 |
0,161 |
| 6 |
0,165 |
0,161 |
| 7 |
0,141 |
0,138 |
| 8 |
0,105 |
0,103 |
| 9 |
0,069 |
0,069 |
On observe que la loi de la variable 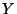 est suffisamment proche
de celle de
est suffisamment proche
de celle de  pour qu'on puisse utiliser la loi de Poisson pour
calculer, par exemple, la probabilité qu'un échantillon de 120 articles
contienne au moins un article défectueux, puis la probabilité que
cet échantillon contienne au plus trois articles défectueux.
pour qu'on puisse utiliser la loi de Poisson pour
calculer, par exemple, la probabilité qu'un échantillon de 120 articles
contienne au moins un article défectueux, puis la probabilité que
cet échantillon contienne au plus trois articles défectueux.
Remarque 1
On admet en général d'utiliser cette approximation lorsque
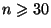
,
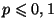
et
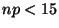
, ou lorsque
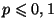
et
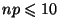
.
Exemple 1
Dans une fabrication en série, 8% des articles présentent des défauts.
Calculer la probabilité que sur 100 contrôles, il y ait 6 articles
défectueux.
On a 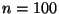 ,
, 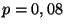 . Nous sommes dans le cas où nous pouvons
approximer la loi binomiale par la loi de Poisson de paramètre
. Nous sommes dans le cas où nous pouvons
approximer la loi binomiale par la loi de Poisson de paramètre
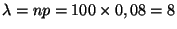 .
On en déduit donc :
.
On en déduit donc :



suivant: Loi normale
monter: Loi de Poisson
précédent: Exemple
Table des matières
Michel
2002-07-27
![]() est suffisamment proche
de celle de
est suffisamment proche
de celle de ![]() pour qu'on puisse utiliser la loi de Poisson pour
calculer, par exemple, la probabilité qu'un échantillon de 120 articles
contienne au moins un article défectueux, puis la probabilité que
cet échantillon contienne au plus trois articles défectueux.
pour qu'on puisse utiliser la loi de Poisson pour
calculer, par exemple, la probabilité qu'un échantillon de 120 articles
contienne au moins un article défectueux, puis la probabilité que
cet échantillon contienne au plus trois articles défectueux.
![]() ,
, ![]() . Nous sommes dans le cas où nous pouvons
approximer la loi binomiale par la loi de Poisson de paramètre
. Nous sommes dans le cas où nous pouvons
approximer la loi binomiale par la loi de Poisson de paramètre
![]() .
On en déduit donc :
.
On en déduit donc :