


suivant: Somme de deux variables
monter: Loi normale
précédent: Loi normale centrée réduite
Table des matières
Théorème 5
On admet que si
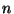
est `` grand ``, et
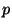
ni trop voisin
de 0, ni trop voisin de 1, alors la loi
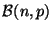
est très
proche de la loi
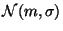
, où
L'intérêt de cette approximation est de simplifier le calculs numériques.
On convient en général d'utiliser cette approximation lorsque 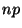 et
et 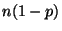 sont supérieurs à 15, ou lorsque
sont supérieurs à 15, ou lorsque 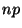 et
et 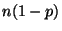 sont
supérieurs à 20.
sont
supérieurs à 20.
Exercice 6
Lançons cinquante fois une pièce de monnaie équilibrée. Soit

la variable aléatoire mesurant le nombre de `` face `` obtenu.
Déterminer la probabilité d'obtenir 25 fois face, en utilisant la
loi binomiale, puis en approximant cette loi par une loi normale.
D'autres exercice dont la correction est à la fin du polycopié :
Exercice 7
Sachant que la variable aléatoire

suit
la loi normale
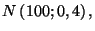
calculer les probabilités
suivantes:
-
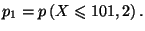
-
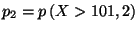
-
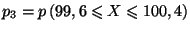
Exercice 8
Sachant que la variable aléatoire
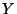
suit
la loi de Poisson de paramètre
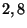
, calculer les probabilités
suivantes:
-
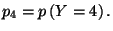
-
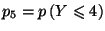
-
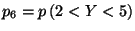
Exercice 9
Dans une salle d'informatique se trouvent huit
ordinateurs. La probabilité que l'un d'eux tombe en panne dans
l'année est de 0,05.
- Quelle est la probabilité
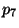 que deux appareils exactement
tombent en panne dans l'année ?
que deux appareils exactement
tombent en panne dans l'année ?
- Quelle est la probabilité
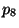 qu'au moins un appareil tombe
en panne dans l'année ?
qu'au moins un appareil tombe
en panne dans l'année ?
Exercice 10
Dans un laboratoire de fabrication de résistances
une étude a montré que la probabilité pour qu'une résistance
tirée au hasard soit défectueuse est
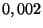
. Une entreprise
achète un lot de 1000 résistances. On note

la variable
aléatoire donnant le nombre de résistances défectueuses
du lot
- Quelle est la loi de probabilité suivie en toute rigueur par
 ? Préciser ses paramètres.
? Préciser ses paramètres.
- On admet que la loi de probabilité
 du lot peut être
approchée par une loi de Poisson de paramètre
du lot peut être
approchée par une loi de Poisson de paramètre 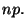 Déduire
de la question précédente le paramètre
Déduire
de la question précédente le paramètre 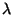 de la loi de Poisson qui lui est substituée.
de la loi de Poisson qui lui est substituée.
- En déduire, en utilisant une table de la loi de Poisson, la probabilité
de l'événement (
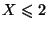 ).
).
Exercice 11
Une machine usine des pièces dont la longueur

exprimée en mm suit une loi normale de moyenne
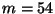
et
d'écart-type
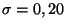
. Une pièce est considérée
comme bonne si
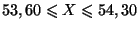
.
- Calculer la probabilité qu'une pièce soit bonne.
- Calculer le pourcentage de pièces défectueuses.
- Pour prévenir un déréglage de la machine on détermine
des cotes d'alerte
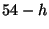 et
et 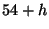 définies par :
Déterminer la valeur de
définies par :
Déterminer la valeur de 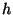 et en déduire ces cotes d'alerte.
On donnera des valeurs approchées à
et en déduire ces cotes d'alerte.
On donnera des valeurs approchées à 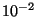 millimètre
près.
millimètre
près.
Exercice 12
Une variable aléatoire

suit une loi normale
de moyenne
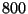
et d'écart-type
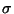
inconnu. Sachant
que
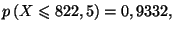
calculer l'écart-type
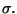



suivant: Somme de deux variables
monter: Loi normale
précédent: Loi normale centrée réduite
Table des matières
Michel
2002-07-27