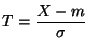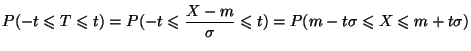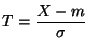
![\includegraphics[]{varf3}](img156.gif)
Le formulaire officiel de mathématiques des classes de bts ne donne
des informations que sur la loi normale centrée réduite. La fonction
de répartition y est notée ![]() . L'aire hachurée sur la courbe
ci-dessus est donc égale à
. L'aire hachurée sur la courbe
ci-dessus est donc égale à ![]() . Pour calculer la probabilité
d'un évènement concernant une variable aléatoire
. Pour calculer la probabilité
d'un évènement concernant une variable aléatoire ![]() suivant la loi
normale centrée réduite, on utilise la table du formulaire et les
deux propriétés suivantes de cette courbe :
suivant la loi
normale centrée réduite, on utilise la table du formulaire et les
deux propriétés suivantes de cette courbe :