Théorème 8
Soit
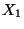
et
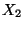
deux variables aléatoires indépendantes
suivant les lois normales respectives
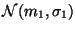
et
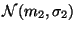
, alors
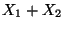
suit la
loi normale de moyenne
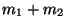
, et d'écart-type
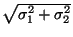
.
Exercice 13
Les deux variables aléatoires

et
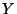
sont indépendantes et suivent respectivement les lois normales
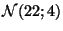
et
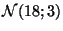
. Soit
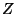
la variable
aléatoire égale à
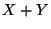
.