



suivant: Forme complexe de la
monter: Séries de Fourier
précédent: Théorème de Dirichlet
Table des matières
Si  est une fonction périodique de période
est une fonction périodique de période 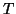 qui satisfait aux
conditions de Dirichlet sur l'intervalle
qui satisfait aux
conditions de Dirichlet sur l'intervalle
![$ \left[ \alpha;\alpha+T\right] $](img2040.gif) ,
où
,
où 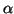 est un réel donné, les coefficients de Fourier se
calculent par :
est un réel donné, les coefficients de Fourier se
calculent par :
En tout point où la fonction  est continue, la somme de la série de
Fourier de
est continue, la somme de la série de
Fourier de  est
est
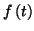 définie par :
En un point
définie par :
En un point 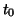 où la fonction
où la fonction  n'est pas continue, la somme de la
série est le réel :
n'est pas continue, la somme de la
série est le réel :
Michel
2002-08-06
![]() est une fonction périodique de période
est une fonction périodique de période ![]() qui satisfait aux
conditions de Dirichlet sur l'intervalle
qui satisfait aux
conditions de Dirichlet sur l'intervalle
![]() ,
où
,
où ![]() est un réel donné, les coefficients de Fourier se
calculent par :
est un réel donné, les coefficients de Fourier se
calculent par :
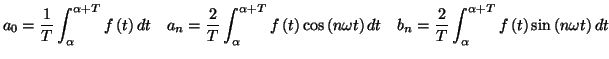
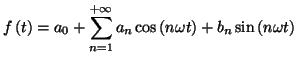
![$\displaystyle \frac{1}{2}\left[ \lim_{t\rightarrow t_{0}^{+}}f\left( t\right)
+\lim_{t\rightarrow t_{0}^{-}}f\left( t\right) \right]
$](img2039.gif)