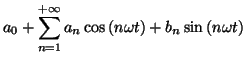suivant: Formule de Parseval
monter: Séries de Fourier
précédent: Forme complexe de la
Table des matières
Si  est une fonction périodique de période
est une fonction périodique de période 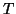 qui satisfait aux
conditions de Dirichlet, sa série de Fourier :
qui satisfait aux
conditions de Dirichlet, sa série de Fourier :
est la somme d'un terme constant 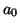 et d'une infinité de fonctions
sinusoïdales
appelées harmoniques de rang
et d'une infinité de fonctions
sinusoïdales
appelées harmoniques de rang  . L'harmonique de rang
. L'harmonique de rang 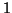 s'appelle
l'harmonique fondamentale.
s'appelle
l'harmonique fondamentale.
Michel
2002-08-06
![]() est une fonction périodique de période
est une fonction périodique de période ![]() qui satisfait aux
conditions de Dirichlet, sa série de Fourier :
qui satisfait aux
conditions de Dirichlet, sa série de Fourier :