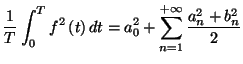suivant: exercices
monter: Séries de Fourier
précédent: Analyse harmonique d'un signal
Table des matières
On démontre que pour une fonction  périodique de période
périodique de période 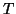 qui satisfait aux conditions de Dirichlet,
qui satisfait aux conditions de Dirichlet,
Michel
2002-08-06
![]() périodique de période
périodique de période ![]() qui satisfait aux conditions de Dirichlet,
qui satisfait aux conditions de Dirichlet,