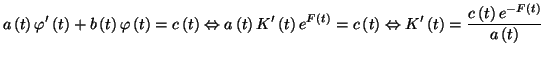suivant: Equations difféntielles linéaires du
monter: Equations différentielles linéaires du
précédent: Cas général
Table des matières
La méthode de Lagrange, aussi appelée méthode de variation de la
constante, permet de déterminer une solution particulière d'une
équation différentielle linéaire du premier ordre, dès lors
que l'on connait la forme générale des solutions de l'équation
homogène associée.
On suppose donc que la solution générale de l'équation
différentielle :
est donnée par
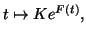 en posant
en posant
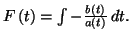 On
recherche alors une solution particulière de la forme
On
recherche alors une solution particulière de la forme
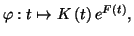 où
où 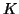 est une fonction
dérivable sur l'intervalle
est une fonction
dérivable sur l'intervalle 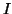 de résolution. En effet, on a :
Il suffit d'intégrer cette dernière équation pour déterminer
de résolution. En effet, on a :
Il suffit d'intégrer cette dernière équation pour déterminer
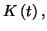 ce qui permet d'obtenir
ce qui permet d'obtenir
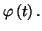
Exercice 8.10
Résoudre l'équation différentielle
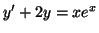 |
(E6) |
Exercice 8.11
Déterminer l'expression de la dérivée sur
![$ \left] 0,\pi\right[ $](img302.gif)
de la fonction
et en déduire la résolution de l'équation différentielle
définie sur
![$ \left] 0,\pi\right[ $](img302.gif)
par
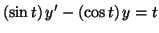 |
(E7) |




suivant: Equations difféntielles linéaires du
monter: Equations différentielles linéaires du
précédent: Cas général
Table des matières
Michel
2002-08-06