Exercice 8.15
Un bassin artificiel destiné à la pisciculture contient 30 000
litres d'eau pure. A un certain moment, une eau polluée à 4 % par
une substance chimique
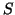
se déverse dans le bassin de façon
continue avec un débit moyen de
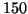
litres à l'heure. On suppose
qu'à partir de ce même moment, le bassin laisse échapper son
contenu avec le même débit. On se propose de déterminer à
chaque instant le pourcentage de substance
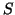
présente dans l'eau du
bassin.
On note
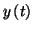 le volume en litres de substance
le volume en litres de substance 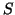 présente à la date
présente à la date 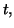 en choisissant comme origine des temps
l'instant où le phénomène de pollution commence, et comme
unité de temps l'heure.
en choisissant comme origine des temps
l'instant où le phénomène de pollution commence, et comme
unité de temps l'heure.
-
Déterminer la quantité de substance 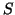 déversée en une
heure dans le bassin.
déversée en une
heure dans le bassin.
- On peut établir que
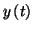 est solution de l'é
quation différentielle
est solution de l'é
quation différentielle
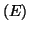
- Déterminer une fonction
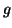 constante solution de
constante solution de
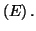
- Montrer que
 est solution de
est solution de
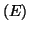 si et seulement si
si et seulement si
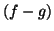 est solution de l'équation
est solution de l'équation
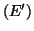 définie par :
définie par :
- Résoudre alors l'équation différentielle
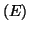
- En déduire l'expression de
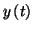 en fonction de
en fonction de 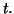
- Calculer le pourcentage
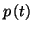 de substance
de substance 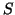 pré
sente dans l'eau du bassin en fonction de
pré
sente dans l'eau du bassin en fonction de 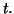
- Quel est le pourcentage maximal de subtance
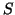 contenue dans le
bassin ?
contenue dans le
bassin ?
- La vie des poissons sera en danger lorsque le taux de substance
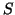 dans l'eau du bassin atteindra 2%. Quel est le temps dont disposera le
pisciculteur pour arrêter cette polution ?
dans l'eau du bassin atteindra 2%. Quel est le temps dont disposera le
pisciculteur pour arrêter cette polution ?
Exercice 8.16
( Sportifs de haut niveau 96 ) L'objectif de la partie A est
de résoudre une équation différentielle
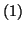 avec second membre. Dans la partie B, on étudiera une fonction,
solution particulière de l'équation
avec second membre. Dans la partie B, on étudiera une fonction,
solution particulière de l'équation
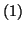 ,
à l'aide d'une fonction auxiliaire. Dans la partie C, on déterminera
l'aire d'une région du plan donnée. Les parties A, B et C peuvent
être traités indépendamment l'une de l'autre.
,
à l'aide d'une fonction auxiliaire. Dans la partie C, on déterminera
l'aire d'une région du plan donnée. Les parties A, B et C peuvent
être traités indépendamment l'une de l'autre.
Résolution d'une équation différentielle.
On se propose de déterminer les fonctions définies sur l'intervalle
![$ \left] 0;+\infty \right[ $](img2284.gif) qui sont solutions de l'équation
différentielle suivante :
qui sont solutions de l'équation
différentielle suivante :
- Montrer que la fonction
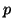 définie sur
définie sur
![$ \left] 0;+\infty \right[ $](img2284.gif) par
par
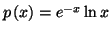 est une solution particulière de
l'équation
est une solution particulière de
l'équation
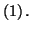
- Démontrer qu'une fonction
 , définie sur
, définie sur
![$ \left] 0;+\infty \right[ $](img2284.gif) est solution de l'équation différentielle
est solution de l'équation différentielle
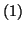 si et seulement si la fonction
si et seulement si la fonction 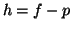 est une solution de l'équation
différentielle :
est une solution de l'équation
différentielle :
- Déterminer les solutions de l'équation différentielle :
- En déduire l'ensemble des solutions de l'équation
différentielle
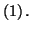
Etude de fonctions
On se propose dans cette partie d'étudier une solution particulière de
l'équation différentielle
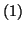 . Soit la fonction
. Soit la fonction  définie sur
définie sur
![$ \left] 0;+\infty \right[ $](img2284.gif) par :
par :
I) Etude d'une fonction auxiliaire
On considère la fonction 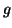 définie sur
définie sur
![$ \left] 0;+\infty \right[ $](img2284.gif) par
:
par
:
- Calculer les limites de
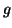 aux bornes de son ensemble de
définition.
aux bornes de son ensemble de
définition.
- Déterminer la fonction dérivée
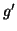 de
de 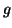 et dresser
le tableau de variation de
et dresser
le tableau de variation de 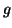 .
.
- Démontrer que l'équation
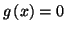 admet une seule
solution
admet une seule
solution 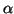 dans
dans
![$ \left] 0;+\infty \right[ $](img2284.gif) et que cette solution
et que cette solution 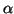 appartient à
appartient à
![$ \left[ 0,45;0,46\right] .$](img2293.gif)
- Déduire de ce qui précède l'étude du signe de
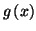 sur
sur
![$ \left] 0;+\infty \right[ .$](img2294.gif)
II) Etude de la fonction  .
.
On note
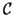 la courbe représentative de
la courbe représentative de  dans un plan
rapporté à un repère orthonormal
dans un plan
rapporté à un repère orthonormal
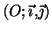 d'unité graphique
d'unité graphique 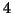 centimètres.
centimètres.
- Etudier les limites de
 aux bornes de son ensemble de dé
finition. Pour calculer la limite de
aux bornes de son ensemble de dé
finition. Pour calculer la limite de  quand
quand 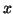 tend vers
tend vers 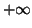 , on
pourra établir que :
, on
pourra établir que :
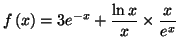 pour tout pour tout 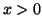 |
|
Déduire de cette étude les asymptotes de la courbe
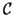 .
.
- Déterminer la fonction dérivée
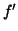 de
de  et v
érifier que, pour tout réel
et v
érifier que, pour tout réel 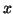 strictement positif, on a :
strictement positif, on a :
Déduire des questions précédentes les variations de  . Pour le
calcul de
. Pour le
calcul de
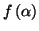 , on prendra comme valeur approchée
de
, on prendra comme valeur approchée
de 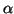 la valeur
la valeur 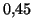 .
.
- Déterminer le point d'intersection de la courbe
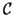 avec l'axe des abscisses.
avec l'axe des abscisses.
- Tracer la courbe
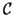 .
.
III) Calcul d'aire
On considère dans le repère orthogonal
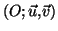 ci-dessous ( unité sur l'axe des abscisses :
ci-dessous ( unité sur l'axe des abscisses : 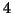 cm, unité
sur l'axe des ordonnées :
cm, unité
sur l'axe des ordonnées : 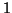 cm ), la courbe de la fonction
cm ), la courbe de la fonction 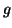 définie par, pour tout
définie par, pour tout 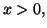
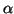
est la valeur déterminée en B.I.3 telle que
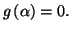
- Déterminer en fonction de
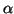 :
:
On pourra utiliser une intégration par parties.
- Calculer, en fonction de
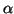 :
:
- Montrer que l'on a :
Exercice 8.17
On se propose de résoudre le système différentiel
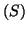
suivant,
puis d'en déterminer une solution particulière.
Les fonctions
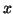
et
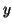
sont des fonctions de la variable réelle
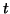
, deux fois dérivables sur

.
Partie A
- Montrer en utilisant les équations
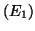 et
et 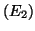 que la
fonction
que la
fonction 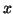 vérifie, pour tout
vérifie, pour tout 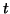 dans
dans
 ,
l'équation différentielle :
,
l'équation différentielle :
- Résoudre sur
 l'équation différentielle
l'équation différentielle 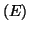 . En
déduire les solutions du système
. En
déduire les solutions du système 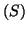 .
.
- Déterminer la solution particulière du système
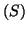 vérifiant les
conditions initiales
vérifiant les
conditions initiales 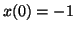 et
et 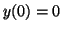 .
.
Partie B
On considère la courbe
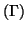
définie par la représentation
paramétrique
où
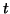
est un réel appartenant à l'intervalle
![$ [-\pi~,~+\pi]$](img2051.gif)
.
- Montrer que la courbe
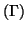 admet un axe de symétrie en
calculant
admet un axe de symétrie en
calculant 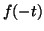 et
et 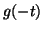 .
.
-
- [2.1]
Calculer
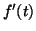 .
.
Montrer que :
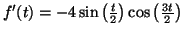 .
.
- [2.2]
Établir le signe de
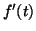 sur l'intervalle
sur l'intervalle ![$ [0~,~\pi]$](img2134.gif) .
.
- On admet que
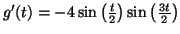 et
que le signe de
et
que le signe de 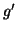 est donné par le tableau suivant :
est donné par le tableau suivant :
Exercice 8.18
PARTIE A : Résolution d'une équation différentielle
On considère l'équation différentielle :
où
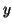
est une fonction de la variable réelle
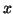
, définie et deux
fois dérivable sur

,
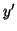
sa fonction dérivée
première et
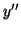
sa fonction dérivée seconde.
- Résoudre sur
 l'équation différentielle :
l'équation différentielle :
- Soit
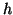 la fonction définie sur
la fonction définie sur
 par :
Démontrer que
par :
Démontrer que 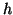 est une solution particulière de l'équation
différentielle
est une solution particulière de l'équation
différentielle
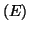 .
.
- En déduire l'ensemble des solutions de l'équation
différentielle
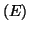 .
.
- Déterminer la solution
 de l'équation différentielle
de l'équation différentielle
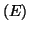 qui vérifie les conditions initiales :
qui vérifie les conditions initiales :
PARTIE B : Etude d'une fonction
Soit  la fonction définie sur
la fonction définie sur
 par :
par :
Sa courbe représentative
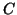
dans un repère orthonormal est donnée
sur la figure ci-après.
- Calculer
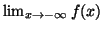 .
.
- Déterminer
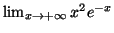 et
et
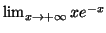 . En déduire
. En déduire
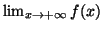 .
.
- Interpréter graphiquement le résultat obtenu au b).
- Démontrer que pour tout
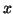 de
de
 ,
,
- Résoudre dans
 l'inéquation
l'inéquation
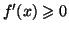 .
.
- En déduire le sens de variation de
 sur
sur
 .
.
- A l'aide du développement limité au voisinage de 0 de la
fonction exponentielle
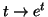 , donner le développement
limité, à l'ordre 2, au voisinage de 0 de la fonction x
, donner le développement
limité, à l'ordre 2, au voisinage de 0 de la fonction x
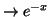 .
.
- Démontrer que le développement limité, à l'ordre 2, au
voisinage de 0 de la fonction f est :
avec
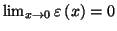 .
.
- En déduire une équation de la tangente
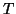 à la courbe
à la courbe 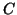 au point d'abscisse 0 et la position relative de
au point d'abscisse 0 et la position relative de 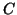 et
et 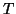 au voisinage de ce point.
au voisinage de ce point.
PARTIE C : Calcul intégral
- La fonction
 définie dans la partie B étant une solution de
l'équation différentielle
définie dans la partie B étant une solution de
l'équation différentielle
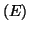 :
montrer que
:
montrer que  vérifie, pour tout
vérifie, pour tout 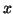 de
de
 :
:
- Soit
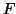 la fonction définie sur
la fonction définie sur
 par :
Vérifier que pour tout
par :
Vérifier que pour tout 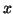 de
de
 ,
,
- Vérifier que pour tout
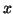 de
de
 :
:
- Utiliser ce qui précède pour démontrer que l'aire
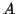 de la
partie du plan hachurée sur la figure est, en unités d'aire,
de la
partie du plan hachurée sur la figure est, en unités d'aire,



 suivant: Solutions des exercices
monter: Equations différentielles
précédent: Equations difféntielles linéaires du
Table des matières
Michel
2002-08-06
suivant: Solutions des exercices
monter: Equations différentielles
précédent: Equations difféntielles linéaires du
Table des matières
Michel
2002-08-06
![]() le volume en litres de substance
le volume en litres de substance ![]() présente à la date
présente à la date ![]() en choisissant comme origine des temps
l'instant où le phénomène de pollution commence, et comme
unité de temps l'heure.
en choisissant comme origine des temps
l'instant où le phénomène de pollution commence, et comme
unité de temps l'heure.
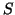 déversée en une
heure dans le bassin.
déversée en une
heure dans le bassin.
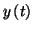 est solution de l'é
quation différentielle
est solution de l'é
quation différentielle
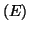
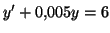
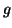 constante solution de
constante solution de
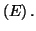
 est solution de
est solution de
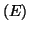 si et seulement si
si et seulement si
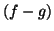 est solution de l'équation
est solution de l'équation
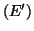 définie par :
définie par :
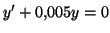
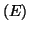
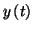 en fonction de
en fonction de 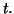
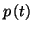 de substance
de substance 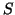 pré
sente dans l'eau du bassin en fonction de
pré
sente dans l'eau du bassin en fonction de 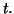
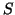 contenue dans le
bassin ?
contenue dans le
bassin ?
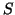 dans l'eau du bassin atteindra 2%. Quel est le temps dont disposera le
pisciculteur pour arrêter cette polution ?
dans l'eau du bassin atteindra 2%. Quel est le temps dont disposera le
pisciculteur pour arrêter cette polution ?
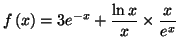 pour tout
pour tout 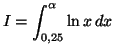
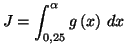
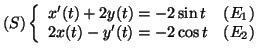
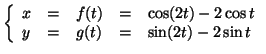
![\includegraphics[]{ts01fig}](img2355.gif)