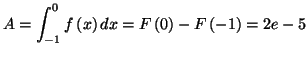suivant: À propos de ce
monter: Equations différentielles
précédent: exercices
Table des matières
Solution 8.1 :
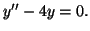
Solution 8.2 : Non, car
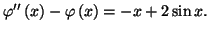
Solution 8.3 : En séparant les variables,
on trouve que les solutions sont les fonctions définies par :
où 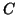 est une constante réelle.
est une constante réelle.
Solution 8.4 :En séparant les variables, on
a sur
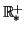 :
:
Par intégration, on trouve comme solutions les fonctions
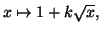 avec
avec 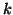 réel.
réel.
Solution 8.5 : On trouve
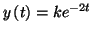 .
.
Solution 8.6 : On trouve
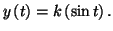
Solution 8.7 : On trouve
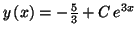
Solution 8.8 : On trouve
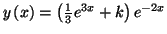 .
.
Solution 8.9 : On trouve :
Solution 8.10 : Les solutions de l'équation
homogène sont
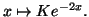 On cherche une solution particuliè
re en posant
On cherche une solution particuliè
re en posant
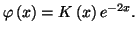 En
reportant dans l'équation différentielle, il vient
En
reportant dans l'équation différentielle, il vient
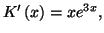 puis
puis
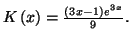 Les solutions de l'équation différentielle sont donc
définies par
Les solutions de l'équation différentielle sont donc
définies par
Solution 8.11 : La fonction
 est dérivable sur
est dérivable sur
![$ \left] 0,\pi\right[ ,$](img2373.gif) de dérivée
de dérivée
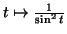 . Les solutions de l'équation homogène
sont les fonctions
. Les solutions de l'équation homogène
sont les fonctions
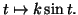 On applique la méthode de Lagrange
pour déterminer une solution particulière. On trouve que :
On applique la méthode de Lagrange
pour déterminer une solution particulière. On trouve que :
Les solutions de l'équation différentielle sont donc :
Solution 8.12 : Par application des formules du
cours :
où 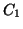 et
et 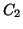 sont deux constantes réelles.
sont deux constantes réelles.
Solution 8.13 : Les solutions de
sont les fonctions 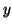 définies par :
définies par :
Solution 8.14 : Les solutions de
sont les fonctions 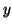 définies par :
La solution vérifiant les conditions proposées est la fonction obtenue
pour
définies par :
La solution vérifiant les conditions proposées est la fonction obtenue
pour
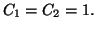
Solution 8.15 :
1. Cette quantité est de
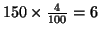 litres.
litres.
2. a) On trouve que
 pour tout
pour tout  réel.
réel.
2. b) Voir cours 2. c) Les solutions de l'équation
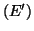 sont
sont
 D'après la question b) on
sait que les solutions de (E) sont donc les fonctions
D'après la question b) on
sait que les solutions de (E) sont donc les fonctions  définies par
définies par
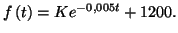
2. d) Comme
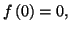 il vient
il vient 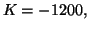 d'où
d'où
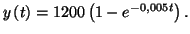
3.
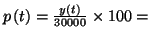
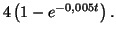
4. La fonction 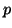 est croissante, donc le maximum s'obtiendra quand
est croissante, donc le maximum s'obtiendra quand  tend vers
tend vers 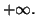 Or, la limite de
Or, la limite de 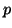 quand
quand  tend vers
tend vers 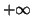 est égale à 4. On en déduit donc que le pourcentage maximal de
subtance
est égale à 4. On en déduit donc que le pourcentage maximal de
subtance 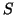 sera donc de 4 %.
sera donc de 4 %.
5.
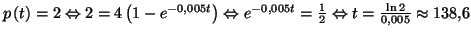 heures.
heures.
Solution 8.16 :
1. Pour tout  de
de
![$ \left] 0;+\infty \right[ $](img2284.gif) , on a :
, on a :
Il suffit alors de vérifier que pour tout  de
de
![$ \left] 0;+\infty \right[ $](img2284.gif) , on a :
, on a :
pour vérifier que 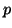 est bien une solution particulière de l'é
quation
est bien une solution particulière de l'é
quation
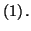
2. Une fonction  , définie sur
, définie sur
![$ \left] 0;+\infty \right[ $](img2284.gif) est
solution de l'équation différentielle
est
solution de l'équation différentielle
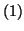 si et
seulement si elle vérifie pour tout
si et
seulement si elle vérifie pour tout  de
de
![$ \left] 0;+\infty \right[ $](img2284.gif) :
:
Par soustraction membre à membre avec l'égalité
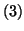 , l'égalité précédente équivaut à :
, l'égalité précédente équivaut à :
Ce qui équivaut au fait que la fonction  est une solution de l'
équation différentielle
est une solution de l'
équation différentielle
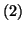 .
.
3. Avec les formules de cours, on trouve que les solutions de l'équation
différentielle
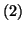 sont les fonctions
sont les fonctions 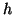 définies
par
définies
par
où 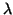 et
et 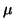 sont deux constantes réelles quelconques.
sont deux constantes réelles quelconques.
4. D'après les questions précédentes, l'ensemble des solutions
de l'équation différentielle
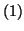 est constitué
par les fonctions
est constitué
par les fonctions  , c'est à dire que cet ensemble de solutions est
constitué des fonctions définies sur
, c'est à dire que cet ensemble de solutions est
constitué des fonctions définies sur
![$ \left] 0;+\infty \right[ $](img2284.gif) par
:
par
:
I) Etude d'une fonction auxiliaire
1.
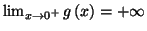 car
car
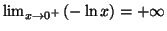 et
et
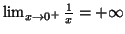 . De même,
. De même,
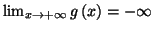 car
car
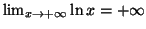 et
et
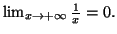
2. Pour tout  de
de
![$ \left] 0;+\infty \right[ $](img2284.gif) on a
on a
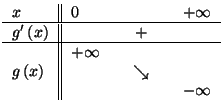
Le signe de
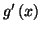 est celui de
est celui de
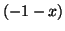 , d'où le tableau de variation de
, d'où le tableau de variation de 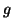 :
:
3. La fonction 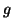 est continue et strictement décroissante sur
est continue et strictement décroissante sur
![$ \left] 0;+\infty \right[ $](img2284.gif) . Elle réalise donc une bijection de
. Elle réalise donc une bijection de
![$ \left] 0;+\infty \right[ $](img2284.gif) sur
sur
![$ \left] -\infty ;+\infty \right[ $](img2410.gif) . Comme 0
appartient à l'intervalle image, l'équation
. Comme 0
appartient à l'intervalle image, l'équation
 admet une seule solution
admet une seule solution 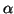 dans
dans
![$ \left] 0;+\infty \right[ $](img2284.gif) . Comme
de plus
. Comme
de plus
 et et  |
|
on en déduit aisément que cette solution 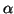 appartient à
appartient à
![$ \left[ 0,45;0,46\right] .$](img2293.gif)
4. La fonction  est décroissante sur
est décroissante sur
![$ \left] 0;\alpha \right[ $](img2413.gif) avec
avec
 , donc
, donc
 est positive sur cet
intervalle. De même, on montre que
est positive sur cet
intervalle. De même, on montre que
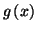 est négative
sur
est négative
sur
![$ \left] \alpha ;+\infty \right[ .$](img2415.gif)
II) Etude de la fonction  .
.
1.
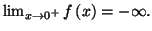 De plus, pour tout
De plus, pour tout
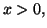 on a :
on a :
Or
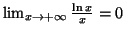 et
et
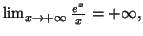 donc
donc
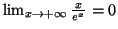 d'après le cours.
d'après le cours.
Donc
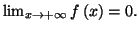 On en déduit que
les droites d'équations
On en déduit que
les droites d'équations 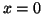 et
et 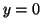 sont asymptotes à
sont asymptotes à
2. Pour tout 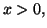
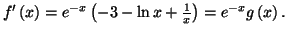 Le signe de
Le signe de
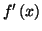 est donc celui de
est donc celui de
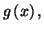 étudi
é précédemment. Donc
étudi
é précédemment. Donc  est croissante sur
est croissante sur
![$ \left] 0;\alpha \right[ $](img2413.gif) et décroissante sur
et décroissante sur
![$ \left] \alpha ,+\infty \right[ .$](img2425.gif) On
trouve que
On
trouve que
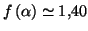 .
.
3.
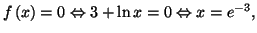 car
car
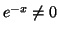 pour tout
pour tout 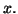 Les coordonnées du point
d'intersection de la courbe
Les coordonnées du point
d'intersection de la courbe
 avec l'axe des abscisses sont
avec l'axe des abscisses sont
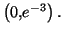 4. Le tracé de
4. Le tracé de 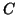 est le suivant :
est le suivant :
III) Calcul d'aire
1.
![$ I=\int_{0,25}^{\alpha }\ln x\,dx=\left[ x\ln x\right] _{0,25}^{\alpha
}-\int_{...
... }dx=\left[ x\ln x\right] _{0,25}^{\alpha }-\left[ x
\right] _{0,25}^{\alpha }.$](img2431.gif) On trouve que :
On trouve que :
2. (a)
![$ J=\left[ -3x\right] _{0,25}^{\alpha }-I+\left[ \ln x\right]
_{0,25}^{\alpha }=-2\alpha +\left( 1-\alpha \right) \ln \alpha +\frac{1}{2}+
\frac{3\ln 2}{2}.$](img2433.gif)
(b) Puisque
 on a
on a
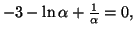 d'où
d'où
 En reportant dans
l'expression de
En reportant dans
l'expression de 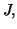 on trouve bien que :
on trouve bien que :
Solution 8.17 :
Partie A
- Dérivons l'équation
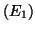 :
De l'équation
:
De l'équation 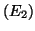 , on tire :
En remplaçant
, on tire :
En remplaçant 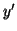 dans l'équation
dans l'équation 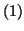 , il vient :
qui est l'équation différentielle
, il vient :
qui est l'équation différentielle 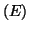 .
.
- L'équation sans second membre a pour équation caractéristique :
dont les solutions sont :
Donc la solution générale de l'équation sans second membre est :
Recherchons maintenant une
solution particulière
 de l'équation complète
de l'équation complète 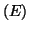 sous la
forme :
donc
sous la
forme :
donc
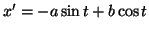 et
et
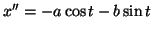 ; en remplaçant dans
; en remplaçant dans 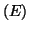 , il vient donc :
Il
faut donc que :
Donc
, il vient donc :
Il
faut donc que :
Donc 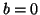 et
et
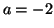 conviennent ; par conséquent
conviennent ; par conséquent
 est une solution
particulière de l'équation complète
est une solution
particulière de l'équation complète 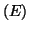 .
.
En conclusion, la
solution générale de l'équation 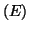 est :
Pour déterminer les solutions
du système
est :
Pour déterminer les solutions
du système 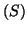 , il reste à calculer
, il reste à calculer 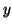 ; on sait que, d'après
; on sait que, d'après 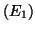 :
On obtient donc, en remplaçant, à l'aide de l'équation
:
On obtient donc, en remplaçant, à l'aide de l'équation  :
:
On vérifie, sans difficulté, en remplaçant dans le système 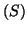 ,
que ces solutions conviennent.
,
que ces solutions conviennent.
En conclusion, la solution de 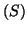 est :
est :
- Déterminons la solution particulière qui satisfait
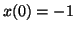 et
et 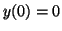 .
Il vient donc :
et
Donc la solution particulière de
.
Il vient donc :
et
Donc la solution particulière de 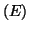 demandée est :
demandée est :
Partie B
-
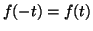 car
car  est pair ;
est pair ;
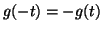 car
car 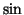 est impair ;
donc la courbe
est impair ;
donc la courbe 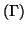 admet l'axe des abscisses pour axe de
symétrie.
admet l'axe des abscisses pour axe de
symétrie.
En effet : si le point
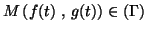 alors
son symétrique par rapport à l'axe des abscisses
alors
son symétrique par rapport à l'axe des abscisses
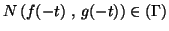 .
.
-
- [2.1] Calculons
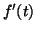 :
:
- [2.2]
Si
 , on a :
, on a :
- d'une part
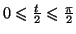 donc
donc
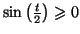
- d'autre part
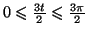 donc il y a deux cas :
En résumé :
donc il y a deux cas :
En résumé :
- On admet que :
ainsi que :
donc le tableau conjoint sur ![$ [0~,~\pi]$](img2134.gif) est :
est :
- Calculons le vecteur tangent
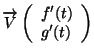 dans les trois cas ci-dessous :
dans les trois cas ci-dessous :
- si
 alors
alors
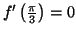 et
et
 donc
donc
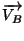 est colinéaire à
est colinéaire à
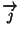 ;
;
- si
 alors
alors
 et
et
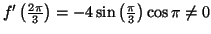 donc
donc
 est colinéaire à
est colinéaire à
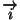 ;
;
- si
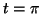 alors
alors
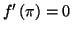 et
et
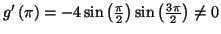 donc
donc
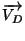 est colinéaire à
est colinéaire à
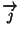 .
.
-
Solution 8.18 :
PARTIE A
- L'équation caractéristique est
qui a pour solution 2 et -1, donc les fonctions
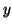 solutions de
l'équation différentielle sont définies sur
solutions de
l'équation différentielle sont définies sur
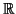 par :
où
par :
où  et
et 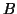 sont deux constantes réelles quelconques.
sont deux constantes réelles quelconques.
- On a :
ce qui permet facilement de vérifier que
ce qui prouve bien que
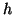 est une solution particulière de l'équation
différentielle
est une solution particulière de l'équation
différentielle
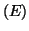 .
.
- D'après le cours, on sait que toute solution de l'équation
différentielle
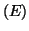 est somme d'une solution
particulière et d'une solution de l'équation
est somme d'une solution
particulière et d'une solution de l'équation
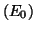 ,
donc toute solution
,
donc toute solution  de
de
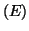 a pour expression :
a pour expression :
- On a facilement :
ce qui donne un système d'équations ayant pour solutions
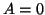 et
et
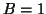 . La fonction
. La fonction  a donc pour expression :
a donc pour expression :
PARTIE B
- On a
- D'après le cours, ou bien à l'aide du changement de variable
défini par
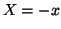 , on a
, on a
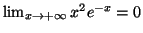 et
et
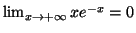 . Il suffit ensuite d'écrire
. Il suffit ensuite d'écrire
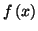 sous la forme :
pour en déduire
sous la forme :
pour en déduire
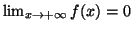 .
.
- On en déduit que la courbe représentative de
 admet une
asymptote horizontale d'équation
admet une
asymptote horizontale d'équation 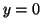 , c'est à dire l'axe des abscisses.
, c'est à dire l'axe des abscisses.
 est dérivable sur
est dérivable sur
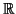 et pour tout
et pour tout  de
de
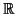 ,
,
- Comme
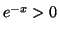 , le signe de
, le signe de
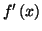 est celui
de
est celui
de
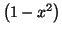 , trinôme qui a deux racines
, trinôme qui a deux racines  et
et 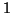 . En
conséquence
. En
conséquence
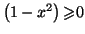 sur
sur
![$ \left[
-1,1\right] $](img634.gif) . Donc
. Donc
![$ \left[
-1,1\right] $](img634.gif) est l'intervalle solution de
l'inéquation
est l'intervalle solution de
l'inéquation
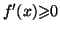 .
.
- On en déduit facilement que
 est décroissante sur
est décroissante sur
![$ \left]
-\infty,-1\right] $](img2524.gif) , croissante sur
, croissante sur
![$ \left[
-1,1\right] $](img634.gif) et
décroissante sur
et
décroissante sur
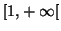 .
.
- On a à l'aide du formulaire :
avec
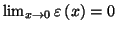 .
.
- Il suffit d'utiliser le produit de deux développements limités
:
en ne conservant dans le développement que les termes d'ordre au plus
égal à deux.
- Une équation de la tangente
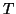 à la courbe
à la courbe 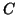 au point
d'abscisse 0 est donc
et comme
on peut en déduire que sur un voisinage de 0, le signe de cette
différence est égal à celui de
au point
d'abscisse 0 est donc
et comme
on peut en déduire que sur un voisinage de 0, le signe de cette
différence est égal à celui de
 , c'est à
dire négatif. En conséquence, on peut dire que la courbe
, c'est à
dire négatif. En conséquence, on peut dire que la courbe 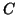 est en
dessous de
est en
dessous de 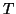 au voisinage de ce point.
au voisinage de ce point.
PARTIE C
- La fonction
 définie dans la partie B étant une solution de
l'équation différentielle
définie dans la partie B étant une solution de
l'équation différentielle
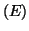 , on peut donc dire que
pour tout
, on peut donc dire que
pour tout  réel :
On isole facilement
réel :
On isole facilement
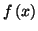 dans un membre pour obtenir
l'égalité demandée :
dans un membre pour obtenir
l'égalité demandée :
- Un simple calcul de dérivation fournit :
et ceci pour tout
 de
de
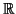 .
.
- On remplace dans l'expression de
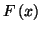
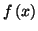 et
et
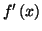 par leurs expressions , ce qui
fournit facilement :
par leurs expressions , ce qui
fournit facilement :
- L'aire
 de la partie du plan hachurée sur la figure est, en
unités d'aire, donnée par l'intégrale
de la partie du plan hachurée sur la figure est, en
unités d'aire, donnée par l'intégrale




suivant: À propos de ce
monter: Equations différentielles
précédent: exercices
Table des matières
Michel
2002-08-06
![]()
![]()
![]() :
:
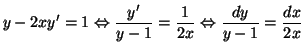
![]() .
.
![]()
![]()
![]() .
.
![]() On cherche une solution particuliè
re en posant
On cherche une solution particuliè
re en posant
![]() En
reportant dans l'équation différentielle, il vient
En
reportant dans l'équation différentielle, il vient
![]() puis
puis
![]() Les solutions de l'équation différentielle sont donc
définies par
Les solutions de l'équation différentielle sont donc
définies par
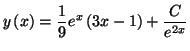
![]() est dérivable sur
est dérivable sur
![]() de dérivée
de dérivée
![]() . Les solutions de l'équation homogène
sont les fonctions
. Les solutions de l'équation homogène
sont les fonctions
![]() On applique la méthode de Lagrange
pour déterminer une solution particulière. On trouve que :
On applique la méthode de Lagrange
pour déterminer une solution particulière. On trouve que :
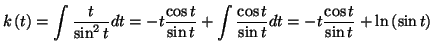
![% latex2html id marker 38188
$\displaystyle \begin{tabular}[c]{l}
$2y^{\prime\pr...
...our solution }y\left( x\right)
=C_{1}e^{x}\sin2x+C_{2}e^{x}\cos2x$\end{tabular}$](img2378.gif)
![]() litres.
litres.
![]() pour tout
pour tout ![]() réel.
réel.
![]() sont
sont
![]() D'après la question b) on
sait que les solutions de (E) sont donc les fonctions
D'après la question b) on
sait que les solutions de (E) sont donc les fonctions ![]() définies par
définies par
![]()
![]() il vient
il vient ![]() d'où
d'où
![]()
![]()
![]()
![]() est croissante, donc le maximum s'obtiendra quand
est croissante, donc le maximum s'obtiendra quand ![]() tend vers
tend vers ![]() Or, la limite de
Or, la limite de ![]() quand
quand ![]() tend vers
tend vers ![]() est égale à 4. On en déduit donc que le pourcentage maximal de
subtance
est égale à 4. On en déduit donc que le pourcentage maximal de
subtance ![]() sera donc de 4 %.
sera donc de 4 %.
![]() heures.
heures.
![]() de
de
![]() , on a :
, on a :
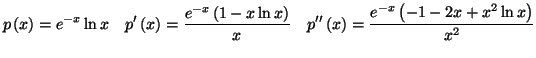
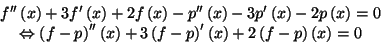
![]() car
car
![]() et
et
![]() . De même,
. De même,
![]() car
car
![]() et
et
![]()
![]() de
de
![]() on a
on a
![]() .
.
![]() De plus, pour tout
De plus, pour tout
![]() on a :
on a :
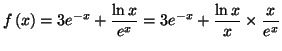
![\includegraphics[]{fig41.eps}](img2430.gif)
![]() On trouve que :
On trouve que :
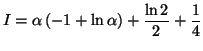
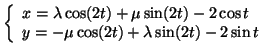
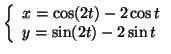
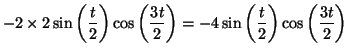

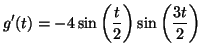
![]() est :
est :
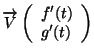 dans les trois cas ci-dessous :
dans les trois cas ci-dessous :
![\includegraphics[scale=1]{courb2.eps}](img2502.gif)
![\begin{displaymath}%%
\begin{array}[c]{c}%%
h^{\prime}\left( x\right) =\left( 2-...
...}\left( x\right) =\left( x^{2}-2x-2\right) e^{-x}%%
\end{array}\end{displaymath}](img2505.gif)

![\begin{displaymath}%%
\begin{array}[c]{c}%%
f\left( x\right) =\left( x^{2}+2x+1\...
...+x-\frac{1}{2}x^{2}+x^{2}\varepsilon\left( x\right)
\end{array}\end{displaymath}](img2527.gif)
![\begin{displaymath}%%
\begin{array}[c]{c}%%
F^{\prime}\left( x\right) =\frac{1}{...
...x\right) +(6x+4)e^{-x}\right] \\
=f\left( x\right)
\end{array}\end{displaymath}](img2532.gif)