



suivant: Dérivabilité
monter: Fonctions d'une variable réelle
précédent: Limites
Table des matières
La continuité en un point est définie de la manière suivante :
Définition 2.3
Soit

une fonction définie sur un intervalle
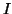
contenant le réel
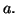
On remarquera que si  est continue en
est continue en 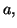 alors
alors
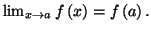
La continuité est très utile pour l'application des théorèmes
relatifs à la résolution des équations du type
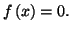
Théorème 2.3 (
des valeurs intermédiaires)
Soit

une fonction continue sur
un intervalle
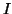
et soient
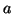
et
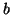
deux éléments de
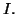
La
fonction

prend toute valeur comprise entre
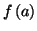
et
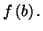
Théorème 2.4
Si

est une fonction continue et strictement monotone sur un intervalle
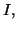
alors elle réalise une bijection de
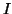
sur
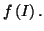
Théorème 2.5
Soit

une fonction continue et strictement monotone sur un intervalle
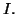
Alors
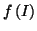
est un intervalle, et pour tout
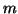
de
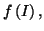
l'équation
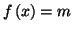
admet une unique solution
dans
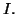
Théorème 2.6
Soit

une fonction continue et strictement monotone sur
![$ \left[
a,b\right] .$](img282.gif)
Si
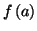
et
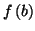
sont de
signes contraires, alors l'équation
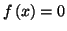
admet une
unique solution dans l'intervalle ouvert
![$ \left] a,b\right[ .$](img285.gif)
Ce théorème justifie la méthode de dichotomie, qui permet de
trouver un encadrement d'une solution d'une équation du type
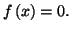
Exercice 2.6
On considère la fonction  définie sur
définie sur
 par :
Cette fonction est-elle continue sur
par :
Cette fonction est-elle continue sur
 ?
?
Définition 2.4
Si une fonction

a une limite réelle
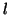
en un point
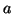
où elle
n'est pas définie, alors on peut la prolonger par continuité en
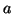
en
posant f
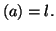
Exercice 2.8
Démontrer que l'équation
admet une unique solution 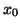 dans
dans
![$ \left[ 0,\pi\right]
$](img297.gif) dont on donnera une valeur approchée à 10
dont on donnera une valeur approchée à 10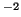 près par défaut.
près par défaut.
 est continue en
est continue en 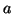 si
si  admet une limite finie en
admet une limite finie en 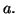
 est continue sur
est continue sur 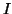 si
si  est continue en
tout point
est continue en
tout point 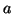 de
de 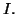
![]() est continue en
est continue en ![]() alors
alors
![]()
![]()
![]()
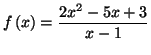 si
si ![\includegraphics[
height=1.8127in,
width=1.8862in
]{capes3.eps}](img301.gif)