- Le rapport
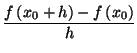 admet une limite finie
admet une limite finie 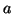 quand
quand 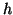 tend vers
tend vers 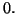
- Pour tout réel
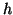 tel que
tel que
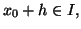 on peut écrire que
on peut écrire que
La notion de dérivée peut être reliée soit aux approximations affines, soit au taux de variation d'une fonction. On rappelle les définitions suivantes :
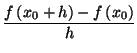 admet une limite finie
admet une limite finie
Attention, la réciproque est fausse. Il suffit par exemple de
considérer la fonction
![]() qui est continue sur
qui est continue sur
![]() mais non dérivable en
mais non dérivable en ![]() Les principales formules de
dérivation sont données à la page
Les principales formules de
dérivation sont données à la page ![[*]](crossref.png) .
.
| Fonctions | Dérivées | Intervalles |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Fonction | Dérivée | Fonction | Dérivée | Fonction | Dérivée |
|
|
|
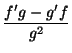 |
|||
|
|
|
|
|
||
Les notions de nombre dérivé à droite et de nombre dérivé
à gauche se définissent en introduisant les limites à droite et
à gauche du taux d'accroissement de ![]() en
en ![]() Sous réserve d'existence de la limite, on pose
:
Sous réserve d'existence de la limite, on pose
:
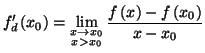
![\begin{displaymath}
\begin{array}[c]{lllll}
\text{a)} & f_{1}\left( x\right) =\d...
...2\cos^{2}\left( \dfrac{\pi}{6}-\dfrac
{x}{4}\right)
\end{array}\end{displaymath}](img364.gif)