



suivant: Exercices
monter: Fonctions usuelles
précédent: Fonctions logarithmes et exponentielles
Table des matières
Définition 3.4
On appelle fonction
sinus hyperbolique la fonction notée
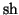
définie sur

par
La courbe représentative de la fonction sinus hyperbolique est :
Définition 3.5
On appelle fonction
cosinus hyperbolique la fonction notée
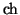
définie sur

par
La courbe représentative de la fonction cosinus hyperbolique est :
Définition 3.6
On appelle fonction
tangente hyperbolique la fonction notée
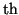
définie sur

par
La courbe représentative de la fonction sinus hyperbolique est :
Les fonctions hyperboliques sont continues sur
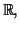 dérivables
sur
dérivables
sur
 et
et
Les fonctions hyperboliques vérifient la relation fondamentale :
Exercice 3.19
Démontrer que :
Exercice 3.20
Déterminer les dérivées des fonctions définies par
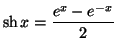
![\includegraphics[scale=0.5]{fig5.ps}](img697.gif)
![\includegraphics[scale=0.5]{fig6.ps}](img700.gif)
![\includegraphics[scale=0.6]{fig7.ps}](img703.gif)
![]() dérivables
sur
dérivables
sur
![]() et
et
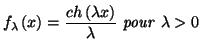
![\includegraphics[]{capes4.eps}](img711.gif)
![$\displaystyle L\left( \lambda\right) =\int_{-1}^{1}\sqrt{1+\left[ f_{\lambda}^{\prime
}\left( x\right) \right] ^{2}}\,dx
$](img717.gif)