Exercice 3.23
On désigne par

un entier supérieur ou égal à 2 et on
considère les fonctions, notées
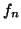
, qui sont définies pour
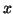
appartenant à l'intervalle
![$ ]0,+\infty\lbrack$](img744.gif)
par :
PARTIE A
I : Etude des fonctions 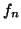
- Calculer
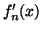 et montrer que l'on peut écrire le
résultat sous la forme d'un quotient dont le numérateur et
et montrer que l'on peut écrire le
résultat sous la forme d'un quotient dont le numérateur et
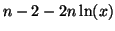 .
.
- Résoudre l'équation
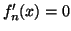 . Etudier le signe de
. Etudier le signe de
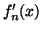
- Déterminer la limite de
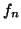 en
en 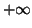
- Etablir le tableau de variation de la fonction
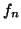 et calculer sa
valeur maximale en fonction de
et calculer sa
valeur maximale en fonction de  .
.
II : Représentation graphique de quelques fonctions 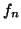
Le plan est rapporté à un repère orthonormal
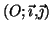 ( unité graphique : 5 cm ). On note
( unité graphique : 5 cm ). On note 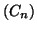 la courbe
représentative de la fonction
la courbe
représentative de la fonction 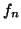 dans ce repère.
dans ce repère.
- Tracer
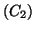 et
et
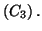
- Calculer
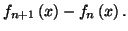 Cette
différence est-elle dépendante de l'entier
Cette
différence est-elle dépendante de l'entier  ?
?
- Expliquer comment il est possible de construire point par point la
courbe
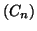 à partir de
à partir de
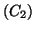 et
et
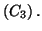
PARTIE B
Calculs d'aires
- Calculer, en intégrant par parties, l'intégrale :
- En déduire l'aire, en unités d'aire, du domaine plan limité
par les courbes
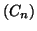 et
et
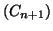 et les
droites d'équations
et les
droites d'équations 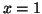 et
et 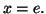
- On note
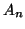 l'aire, en unités d'aire, du domaine limité par
la courbe
l'aire, en unités d'aire, du domaine limité par
la courbe
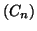 et les droites d'équations
et les droites d'équations 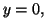
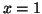 et
et 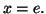
- Calculer
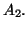
- Déterminer la nature de la suite
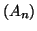 en
précisant l'interprétation graphique de sa raison.
en
précisant l'interprétation graphique de sa raison.
PARTIE C
Etude sur l'intervalle
![$ \left] 1;+\infty\right[ $](img762.gif) de
l'équation
de
l'équation
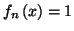 .
.
Dans toute la suite, on prendra
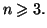
- Vérifier que, pour tout
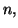
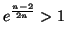
et
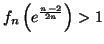
- Vérifier que l'équation
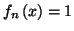 n'a pas de
solution sur l'intervalle
n'a pas de
solution sur l'intervalle
![$ \left] 1;e^{\frac{n-2}{2n}}\right[ .$](img767.gif)
- Montrer que l'équation
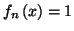 admet sur
l'intervalle
admet sur
l'intervalle
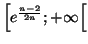 exactement une
solution notée
exactement une
solution notée
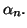
- On se propose de déterminer la limite de la suite
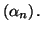
- Calculer
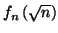 et montrer que, pour
et montrer que, pour
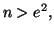 on a
on a
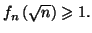
- En déduire que, pour
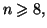 on a
on a
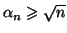 et donner la limite de la suite
et donner la limite de la suite
Exercice 3.24
Le plan est muni d'un repère orthonormal
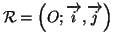 . L'unité graphique est
. L'unité graphique est
 cm.
cm.
PARTIE A
Soit  la fonction définie sur
la fonction définie sur
 par
par
Soit
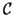
la courbe représentative de

dans le repère
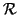
.
- Déterminer les limites de
 aux bornes de son ensemble de définition.
aux bornes de son ensemble de définition.
- Etudier le sens de variation de
 et donner le tableau de variation
de
et donner le tableau de variation
de  .
.
- Tracer
 .
.
- Soit
- Interpréter graphiquement
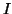 .
.
- En utilisant l'intégration par parties, calculer
puis
- En déduire la valeur exacte de
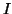 .
.
PARTIE B
- Soit
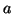 et
et 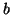 deux nombres réels et
deux nombres réels et 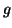 la fonction définie
sur
la fonction définie
sur
 par
Quelles sont les valeurs de
par
Quelles sont les valeurs de 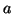 et de
et de 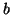 pour lesquelles le tableau de
variation de
pour lesquelles le tableau de
variation de 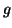 est celui donné ci-dessous ?
est celui donné ci-dessous ?
- Soit
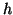 la fonction définie sur
la fonction définie sur
 par
et
par
et 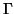 sa courbe représentative dans le repère
sa courbe représentative dans le repère
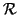 .
.
- Démontrer que la droite
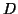 d'équation
d'équation
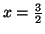 est axe
de symétrie de
est axe
de symétrie de 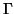 .
.
- Justifier l'affirmation suivante : '' 3,2 est une valeur approchée
à
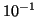 près d'une solution de l'équation
près d'une solution de l'équation
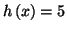 ''
''
- Soit
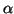 un nombre dont 1,7 est une valeur approchée à 0,5
près. Etablir que
un nombre dont 1,7 est une valeur approchée à 0,5
près. Etablir que
PARTIE C
Soit 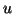 une fonction dérivable sur
une fonction dérivable sur
 dont le tableau de
variation est donné ci-dessous (
dont le tableau de
variation est donné ci-dessous ( 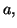
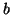 et
et 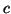 étant trois nombres
réels ).
étant trois nombres
réels ).
Soit
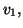
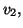
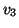
les fonctions définies par :
- Déterminer le sens de variation des fonctions
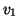 et
et 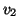 (
en justifiant votre réponse ).
(
en justifiant votre réponse ).
- Indiquer un intervalle sur lequel il est possible de donner le sens de
variation de la fonction
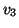 ( en justifiant votre réponse ).
( en justifiant votre réponse ).
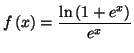
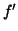 de
de
 sur
sur
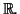 Montrer que pour tout
Montrer que pour tout 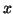 ré
el,
ré
el,
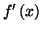 est du signe de
est du signe de
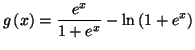
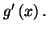
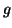 aux bornes de son
domaine de définition.
aux bornes de son
domaine de définition.
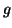 , puis
déduire des questions précédentes le signe de
, puis
déduire des questions précédentes le signe de
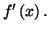
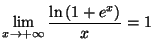
 en
en 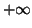 et
en
et
en 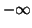 .
.
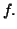
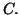
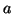 et
et 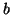 tels que
pour tout réel
tels que
pour tout réel 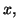 on ait :
on ait :
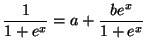
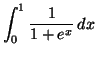
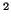 l'aire de la portion du plan comprise entre les droites
d'équation
l'aire de la portion du plan comprise entre les droites
d'équation 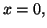
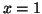 ,
, 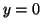 et la courbe
et la courbe 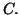
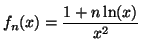
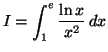
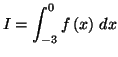
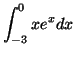
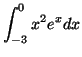
![$\displaystyle %%
\begin{tabular}[c]{l\vert lllll}%%
$x$\ & $-\infty$\ & & $\fra...
...& $\searrow$\ & & $\nearrow$\ & \\
& & & $e^{-\frac{5}{4}}$\ & &
\end{tabular}$](img783.gif)
![$\displaystyle %%
\begin{tabular}[c]{l\vert ccccccccc}%%
$x$\ & $-\infty$\ & & $...
... & & $\searrow$\ & & $\nearrow$\ & & & \\
& & & & & $c$\ & & & &
\end{tabular}$](img790.gif)