Solution 3.1 : A l'aide des formules
trigonométriques donnant
![]() et
et
![]() on trouve facilement que
on trouve facilement que ![]() et
et ![]()
Solution 3.2 : On écrit l'égalité
entre deux sinus ou entre deux cosinus. Si ![]() est l'ensemble des solutions,
on a :
est l'ensemble des solutions,
on a :
Solution 3.3 : Par les formules trigonomé
triques, on a :

Solution 3.4 : On obtient par les formules
trigonométriques :
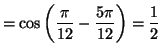 |
||
Solution 3.5 :On factorise par
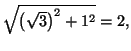 de qui donne
de qui donne

Solution 3.6 : Comme
![]()
![]() et donc
et donc
![]() On en déduit que
On en déduit que

Solution 3.7 : 1) La décomposition
![]() donne
donne
2) a)
![]()
![\includegraphics[scale=0.6]{fig11.ps}](img822.gif)
c) Comme ![]() réalise une bijection de
réalise une bijection de
![]() sur
sur
![]() et que
et que
![]() il est donc légitime de poser
il est donc légitime de poser
![]() L'équation se transforme en
L'équation se transforme en
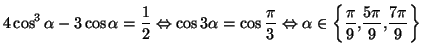
Solution 3.8 : Remarquons que :
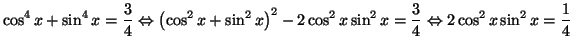
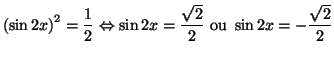
Solution 3.9 : 2)
![]() donc
donc
![]() sur
sur
![]() et
et
![]() sur
sur
![]()
3)
![]() On
en déduit à l'aide d'un tableau de signes que
On
en déduit à l'aide d'un tableau de signes que ![]() est croissante sur
est croissante sur
![]() et
décroissante sur
et
décroissante sur
![]()
Solution 3.10 : On trouve que
![]() pour tout
pour tout ![]() de
de
![]() Comme
Comme
![]() on a donc
on a donc
![]() pour
tout
pour
tout ![]() de
de
![]()
Solution 3.12 :
Solution 3.13 : Le domaine de définition est
égal à
![]() La fonction
La fonction ![]() est
dérivable sur son domaine, avec
est
dérivable sur son domaine, avec
![]() Sa courbe représentative a pour allure
Sa courbe représentative a pour allure
Solution 3.14 : a)Le système
équivaut à
![\begin{displaymath}\left\{
\begin{array}[c]{l}
xy=e^{-1}\\
\frac{x}{y}=e^{5}
\end{array}\right. \end{displaymath}](img856.gif) avec
avec ![]() et
et ![]() On obtient alors
On obtient alors ![]() et
et ![]()
b) Le système équivaut à
![\begin{displaymath}\left\{
\begin{array}[c]{l}
x^{2}+y^{2}=169\\
xy=60
\end{array}\right. \end{displaymath}](img861.gif) avec
avec ![]() et
et ![]() On obtient alors
On obtient alors
![]() et
et
![]() comme couple de solutions.
comme couple de solutions.
Solution 3.15 : a) Le domaine de définition
est
![]() On a
On a
b)
![]() donc
donc
![]()
Solution 3.16 :Domaine de définition :
![]()
La stricte croissante de la fonction logarithme permet d'affirmer que l'équation proposée est équivalente à
![$\displaystyle \frac{x+1}{3x-5}\geqslant1\Leftrightarrow\frac{-2x+6}{3x-5}\geqslant
0\Leftrightarrow x\in\left] \frac{5}{3},3\right]
$](img872.gif)
Solution 3.17 : On pose ![]() d'où une
solution qui est
d'où une
solution qui est ![]()
Solution 3.18 : On pose ![]() et
et ![]() d'où
d'où ![]() et
et ![]()
Solution 3.19 : En utilisant la définition,
on a :
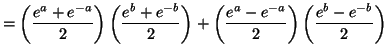 |
||
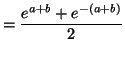 |
||
Solution 3.22 :
1.
![]() =
=
![]() Comme
Comme ![]() pour tout
pour tout ![]() de
de
![]()
![]() et
et
![]() sont bien de même signe.
sont bien de même signe.
2. (a)
![]() (b)
(b)
![]() De manière évidente, on a
De manière évidente, on a
![]()
![]() .
.
(c)
![]() donc
donc ![]() est strictement décroissante
sur
est strictement décroissante
sur
![]() Comme
Comme
![]() la fonction
la fonction ![]() est donc à
valeurs négatives.
est donc à
valeurs négatives.
3. (a)
![]() donc
donc
![]()
(b)
![]() en posant
en posant
![]()
![]()
(c)
![]() est du signe
de
est du signe
de
![]() qui est négatif, donc
qui est négatif, donc ![]() est décroissante
sur
est décroissante
sur
![]()
4. (a) ![]() et
et ![]() (b) On a donc
(b) On a donc
![$\displaystyle \int_{0}^{1}\frac{1}{1+e^{x}}\,dx=\int_{0}^{1}\left( 1-\frac{e^{x...
...eft( 1+e^{x}\right) \right] _{0}^{1}
=\allowbreak-\ln\left( 1+e\right) +1+\ln2
$](img901.gif)
 |
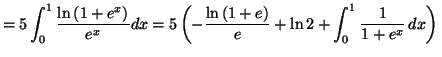 |
|
![\includegraphics[]{fig14.ps}](img907.gif)
Solution 3.23 :
PARTIE A
I) 1)
![]() Le signe de
Le signe de
![]() est celui de
est celui de
![]() car
car ![]() sur
sur
![]()
2)
![]() Remarquons que cette valeur est strictement positive, donc elle appartient au
domaine de définition de
Remarquons que cette valeur est strictement positive, donc elle appartient au
domaine de définition de ![]()
Sur
![]()
![]() donc
donc
![]() donc
donc ![]() est strictement croissante.
est strictement croissante.
De même,
![]() est strictement décroissante sur
est strictement décroissante sur
![]()
3)
![]() car d'après le cours,
car d'après le cours,
![]() et
et
![]()
4)
| 0 |
|
||||
|
|
0 | ||||
|
|
|||||
|
|
|||||
| 0 |
II) 1) ![]() est en trait plein, et
est en trait plein, et ![]() en pointillés.
en pointillés.
![\includegraphics[
height=2.0539in,
width=3.0727in
]{fig40.eps}](img931.gif)
2) (a)
![]() Cette différence est indépendante de
Cette différence est indépendante de ![]()
(b) On a
![]() donc
donc
![]() On appelle
On appelle ![]()
![]() et
et
![]() les points de
les points de ![]()
![]() et
et ![]() d'abscisses
d'abscisses ![]()
![]() est
donc le milieu de
est
donc le milieu de
![]() ce qui prouve que l'on
obtient
ce qui prouve que l'on
obtient ![]() comme symétrique de
comme symétrique de ![]() par rapport à
par rapport à ![]()
PARTIE B
1)
![]()
2) Sur
![]()
![]() donc
donc
![]() donc
donc ![]() est située au-dessus de
est située au-dessus de ![]() donc l'aire cherchée est égale en unités d'aire à
donc l'aire cherchée est égale en unités d'aire à
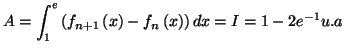
![$\displaystyle A_{2}=\int_{1}^{e}f_{2}\left( x\right) \,dx=\int_{1}^{e}\frac{1}{x^{2}
}+2\frac{\ln x}{x^{2}}\,dx=\left[ -\frac{1}{x}\right] _{1}^{e}+2I=3-5e^{-1}
$](img952.gif)
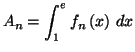
PARTIE C
1) a) Pour
![]()
![]() donc
donc
![]() Comme la fonction
Comme la fonction ![]() est croissante sur
est croissante sur
![]() on a donc
on a donc
![]() Comme
Comme
![]() le résultat est évident.
le résultat est évident.
b) ![]() est strictement croissante
sur
est strictement croissante
sur
![]() et
et
![]() donc
donc
![]() sur
sur
![]() ce qui prouve bien que l'équation
ce qui prouve bien que l'équation
![]() ne peut pas
avoir de solution sur cet intervalle.
ne peut pas
avoir de solution sur cet intervalle.
2) La fonction ![]() est
dérivable et strictement décroissante sur
est
dérivable et strictement décroissante sur
![]() Elle définit donc une bijection de cet intervalle sur
Elle définit donc une bijection de cet intervalle sur
![]() Comme
Comme
![]() il existe
il existe
![]() unique
solution de
unique
solution de
![]() sur cet intervalle.
sur cet intervalle.
3) (a)
![]() car
car
![]() Si
Si ![]() alors
alors
![]() et donc
et donc
![]() puisque
puisque
![]()
(b) Si
![]() alors
alors ![]() puisque
puisque
![]() donc
donc
![]() ce qui implique que
ce qui implique que
![]() car l'on sait que
car l'on sait que ![]() strictement décroissante sur
strictement décroissante sur
![]() . On en déduit aisément que
. On en déduit aisément que
Solution 3.24 : PARTIE A
![$\displaystyle %%
\begin{tabular}[c]{l\vert ccccccc}%%
$x$\ & $-\infty$\ & & $-1...
... & $\searrow$\ & & $\nearrow$\ & \\
& $0$\ & & & & $-e^{2}$\ & &
\end{tabular}$](img987.gif)
![\includegraphics[]{d2sf1}](img988.gif)
![$\displaystyle \int_{-3}^{0}xe^{x}dx=\left[ xe^{x}\right] _{-3}^{0}-\int_{-3}^{0...
...x}dx=\left[ xe^{x}\right] _{-3}^{0}-\left[ e^{x}\right] _{-3}%%
^{0}=4e^{-3}-1
$](img993.gif)
![$\displaystyle \int_{-3}^{0}x^{2}e^{x}dx=\left[ x^{2}e^{x}\right] _{-3}^{0}-\int...
...x}dx=\left[ x^{2}e^{x}\right] _{-3}^{0}-2\int_{-3}^{0}%%
xe^{x}dx=2-17e^{-3}%%
$](img995.gif)
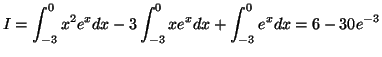
PARTIE B
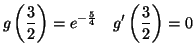
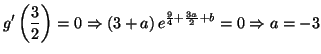
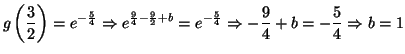
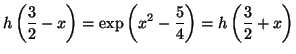
PARTIE C