suivant: Exercices
monter: Les outils de l'analyse
précédent: Développement limité et continuité
Table des matières
Définition 4.5
Soit

une fonction définie sur un voisinage de
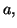
et

un entier
naturel. On dit que la fonction

admet
un développement
limité à l'ordre  au voisinage de
au voisinage de 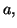
s'il existe un
polynôme
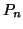
de degré inférieur ou égal à

tel que
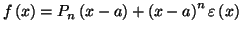
avec
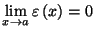
On écrira dans ce cas :
Théorème 4.8
La fonction

admet un développement limité à l'ordre

au
voisinage de
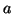
si et seulement si la fonction
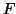
définie par
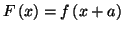
admet un développement limité à
l'ordre

au voisinage de
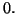
Ce théorème permettra d'obtenir un développement limité au
voisinage d'un point 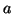 en effectuant le changement de variable défini
par
en effectuant le changement de variable défini
par 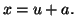 Lorsque
Lorsque 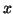 est au voisinage de
est au voisinage de 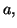
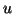 est au voisinage de
est au voisinage de 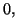 ce qui permet d'utiliser tous les résultats précédents.
ce qui permet d'utiliser tous les résultats précédents.
Exercice 4.20
Déterminer le développement limité de
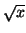
au voisinage de
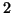
à l'ordre
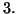
Exercice 4.21
Déterminer le développement limité de la fonction

définie
par
à l'ordre
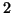
au voisinage de
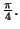
On rappelle la formule
trigonométrique :




suivant: Exercices
monter: Les outils de l'analyse
précédent: Développement limité et continuité
Table des matières
Michel
2002-08-06
![]() en effectuant le changement de variable défini
par
en effectuant le changement de variable défini
par ![]() Lorsque
Lorsque ![]() est au voisinage de
est au voisinage de ![]()
![]() est au voisinage de
est au voisinage de ![]() ce qui permet d'utiliser tous les résultats précédents.
ce qui permet d'utiliser tous les résultats précédents.