



suivant: Suites arithmétiques et géométriques
monter: Definitions
précédent: Génération par récurrence
Table des matières
Exercice 6.7
Soit
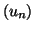 la suite définie par
la suite définie par
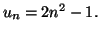 Exprimer en fonction de
Exprimer en fonction de 
Exercice 6.8
Si pour tout entier  on a
on a
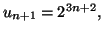 que
vaut alors
que
vaut alors 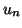 pour
pour
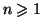 ?
?
Exercice 6.9
On définit la suite
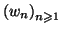 par la relation :
Exprimer
par la relation :
Exprimer
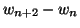 en fonction de
en fonction de 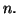
Michel
2002-08-06