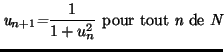
Le calcul du ![]() ième terme d'une suite récurrente suppose que tous
les termes d'indices inférieurs soient connus, ce qui n'est pas
nécessaire pour une suite dans laquelle
ième terme d'une suite récurrente suppose que tous
les termes d'indices inférieurs soient connus, ce qui n'est pas
nécessaire pour une suite dans laquelle ![]() s'exprime en fonction de
s'exprime en fonction de ![]()
Pour une suite définie par son premier terme et la relation de
récurrence
![]() on prendra garde au fait que
le sens de variation de la fonction
on prendra garde au fait que
le sens de variation de la fonction ![]() ne correspond pas forcément à
celui de la suite, comme le montre l'exemple suivant, obtenu en choisissant
ne correspond pas forcément à
celui de la suite, comme le montre l'exemple suivant, obtenu en choisissant
![]() et
et ![]() définie sur
définie sur
![]() par
par
![]()
![\includegraphics[]{capes1.eps}](img1656.gif)
La fonction ![]() est décroissante, mais la suite
est décroissante, mais la suite
![]() n'est ni croissante, ni décroissante.
n'est ni croissante, ni décroissante.