suivant: Comportement asymptotique
monter: Suites numériques
précédent: Suites géométriques
Table des matières
On révisera dans ce chapître les notions de suites majorée,
minorée, bornée, croissante et décroissante. Il existe
différentes techniques d'étude du sens de variation d'une suite :
Exercice 6.15
Etudier la monotonie des suites définies par
Exercice 6.16
Montrer que chacune des suites ci-dessous est bornée :
Exercice 6.17
A l'aide d'un raisonnement par récurrence, déterminer le sens de
variation des suites
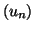 et
et
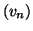 définies par
définies par
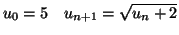
et
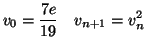
Michel
2002-08-06