Suites adjacentes

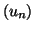
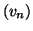
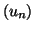
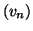
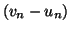
Définition 6.7   Deux suites $\left( u_{n}\right)$ et $\left( v_{n}\right)$ sont dites adjacentes si la suite $\left( u_{n}\right)$ est croissante, la suite $\left( v_{n}\right)$ est décroissante et si $\left( v_{n} -u_{n}\right)$ tend vers 0 quand $n$ tend vers l'infini.

Une des conséquences de cette définition est que pour tout $n$ de $\mathbb{N},$ $u_{n}\leqslant v_{n}.$

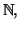
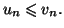
Théorème 6.7   Deux suites adjacentes sont convergentes et convergent vers la même limite.

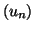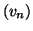Exercice 6.21   On considère les suites $\left( u_{n}\right)$ et $\left( v_{n}\right)$ définies par :

$$u_{n}=\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{2n}\qquad v_{n}=u_{n} +\frac{1}{n}$$

Vérifier que ces deux suites sont adjacentes.