



suivant: Exercices
monter: Suites numériques
précédent: Suites adjacentes
Table des matières
Définition 6.8
Soient
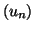
et
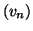
deux suites. On
dit que
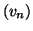
est
extraite de
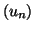
s'il existe une application
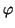
strictement croissante
de
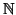
dans
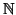
telle que
On dit aussi que
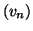 est une sous-suite de
est une sous-suite de
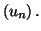 Par exemple, la suite
Par exemple, la suite
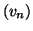 définie
par
définie
par
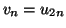 pour tout
pour tout  est une suite extraite de la suite
est une suite extraite de la suite
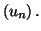
Proposition 6.5
Si
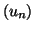
est une suite convergente, alors toute suite
extraite de
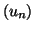
est convergente vers la même limite.
Proposition 6.6
Si les suites
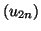
et
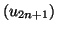
convergent vers la même limite
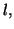
alors la suite
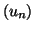
est convergente vers
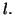
Remarque : On considère la suite
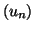 définie par :
définie par :
Vérifier que les suites
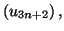
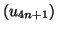 et
et
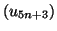 sont convergentes, et que la
suite
sont convergentes, et que la
suite
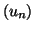 est divergente.
est divergente.
Michel
2002-08-06
![]() est une sous-suite de
est une sous-suite de
![]() Par exemple, la suite
Par exemple, la suite
![]() définie
par
définie
par
![]() pour tout
pour tout ![]() est une suite extraite de la suite
est une suite extraite de la suite
![]()
![]() définie par :
définie par :
![\begin{displaymath}
\left\{
\begin{array}[c]{l}
u_{n}=0\text{ si }n\text{ n'est ...
...{n}=1\text{ si }n\text{ est multiple de }60
\end{array}\right.
\end{displaymath}](img1731.gif)