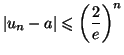Exercice 6.22
Le plan complexe est rapporté à un repère orthonormal direct
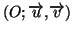
( unité
graphique : 6 cm ). On considère la suite
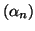
de
nombres réels définie par
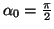
et pour tout
entier naturel
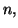
Pour tout entier naturel
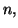
on appelle
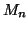
le point du cercle
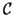
de centre
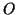
de rayon
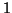
tel que l'angle
ait pour mesure
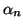
.
- Placer les douze points
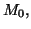
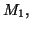
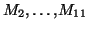 .
.
- On appelle
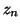 l'affixe de
l'affixe de 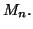 Montrer que pour tout entier
naturel
Montrer que pour tout entier
naturel 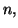 on a l'égalité :
on a l'égalité :
- Montrer pour tout entier naturel
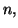 les propriétés suivantes :
les propriétés suivantes :
- Montrer que pour tout entier naturel
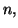 on a l'égalité :
En déduire que la distance
on a l'égalité :
En déduire que la distance
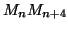 vaut
vaut 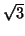 puis que le
triangle
puis que le
triangle
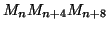 est équilatéral.
est équilatéral.
On admettra
que tous les triangles équilatéraux ayant pour sommets des points
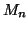 sont de la forme
sont de la forme
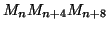 .
.
- Douze cartons indiscernables au toucher, marqués
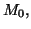
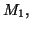
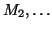 ,
, 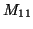 sont disposés dans une urne. On tire au hasard et
simultanément trois cartons de l'urne. Calculer la probabilité
d'obtenir les trois sommets d'un triangle équilatéral.
sont disposés dans une urne. On tire au hasard et
simultanément trois cartons de l'urne. Calculer la probabilité
d'obtenir les trois sommets d'un triangle équilatéral.
Exercice 6.26
Partie A
Soit

la fonction définie sur

par :
On note
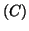
la courbe représentative de

dans un repère
orthonormal
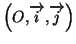
.
On prendra 5 cm comme unité.
- Déterminer la limite de
 en
en 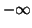 .
.
- Vérifier que pour tout réel
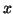 non nul :
Déterminer la limite de
non nul :
Déterminer la limite de  en
en 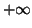 .
.
- Déterminer
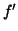 . Etudier le signe de
. Etudier le signe de
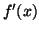 et
calculer la valeur exacte du maximum de
et
calculer la valeur exacte du maximum de  .
.
- Démontrer que la droite
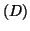 d'équation :
d'équation : 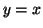 est asymptote
à la courbe
est asymptote
à la courbe 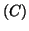 .
.
Etudier la position relative de 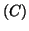 et de
et de
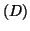 .
.
- On note
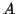 le point de la courbe
le point de la courbe 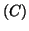 d'abscisse 1.
d'abscisse 1.
Déterminer une équation de la tangente 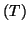 en
en 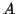 à la courbe
à la courbe
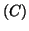 .
.
- On note
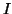 l'intervalle
l'intervalle ![$ [0; 0,5]$](img1785.gif) .
.
Démontrer que
l'équation : 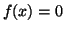 admet dans l'intervalle
admet dans l'intervalle 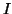 une unique solution
qu'on notera
une unique solution
qu'on notera 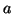 .
.
- Déterminer une valeur approchée à
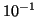 près de
près de 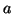 .
.
- Construire la courbe
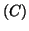 , l'asymptote
, l'asymptote 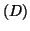 et la tangente
et la tangente 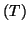 .
.
Partie B
Détermination d'une valeur approchée
de
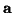
On définit dans
 la suite
la suite 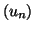 par :
par :
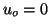
et
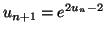
- Soit
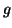 la fonction définie sur
la fonction définie sur
 par :
par :
Démontrer que l'équation : 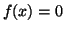 est équivalente à
:
est équivalente à
: 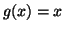 .
.
En déduire 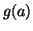 .
.
- Démontrer que, pour tout réel
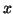 de l'intervalle
de l'intervalle 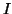 on a :
on a :
- Démontrer que pour tout réel
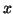 de l'intervalle
de l'intervalle 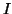 ,
, 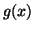 appartient à
appartient à 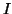 .
.
- Utiliser l'inégalité des accroissements finis pour
démontrer que, pour tout entier naturel
 :
:
- Démontrer, par récurrence que :
- En déduire que la suite
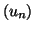 converge et donner sa limite.
converge et donner sa limite.
- Déterminer un entier naturel
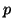 tel que :
tel que :
- En déduire une valeur approchée de
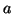 à
à 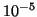 près
: on expliquera l'algorithme utilisé sur la calculatrice.
près
: on expliquera l'algorithme utilisé sur la calculatrice.
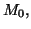
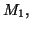
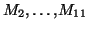 .
.
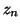 l'affixe de
l'affixe de 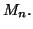 Montrer que pour tout entier
naturel
Montrer que pour tout entier
naturel 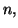 on a l'égalité :
on a l'égalité :
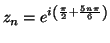
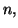 les propriétés suivantes :
les propriétés suivantes :
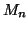 et
et 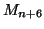 sont diamétralement opposés;
sont diamétralement opposés;
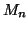 et
et 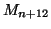 sont confondus.
sont confondus.
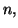 on a l'égalité :
En déduire que la distance
on a l'égalité :
En déduire que la distance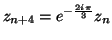
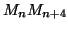 vaut
vaut 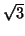 puis que le
triangle
puis que le
triangle
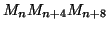 est équilatéral.
est équilatéral.
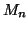 sont de la forme
sont de la forme
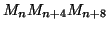 .
.
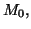
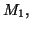
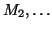 ,
, 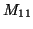 sont disposés dans une urne. On tire au hasard et
simultanément trois cartons de l'urne. Calculer la probabilité
d'obtenir les trois sommets d'un triangle équilatéral.
sont disposés dans une urne. On tire au hasard et
simultanément trois cartons de l'urne. Calculer la probabilité
d'obtenir les trois sommets d'un triangle équilatéral.
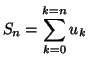
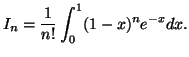
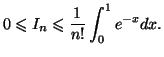
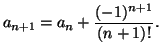
![$\displaystyle f(x)=x\,\left[ 1-2e^{-2}\times\left( \frac{e^{2x}}{2x}\right) \right]
$](img1780.gif)