suivant: Séries numériques
monter: Suites numériques
précédent: Exercices
Table des matières
Solution 6.1 Le tableau suivant donne les valeurs
demandées :
Solution 6.3 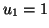
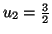
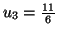
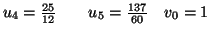
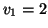
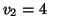
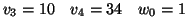
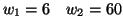
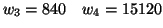 .
.
Solution 6.4 Le programme suivant en basic réalise
l'opération :
Sur la TI81, le programme s'écrit avec la syntaxe suivante :
| |
 INPUT INPUT  Lbl1 : Lbl1 :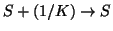 |
|
| |
 IS IS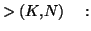 Goto 1 :Disp Goto 1 :Disp 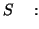 End End |
|
Solution 6.5 
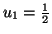
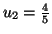
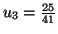
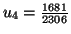
Solution 6.7

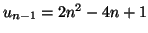

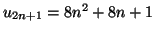
Solution 6.8
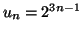
Solution 6.9
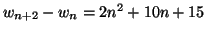
Solution 6.10
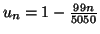
Solution 6.11 a)
 c) On trouve que
c) On trouve que 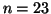
Solution 6.12 On forme :
Solution 6.13 On montre que pour tout 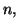
On en déduit que
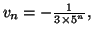 puis que
puis que
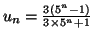
Solution 6.14
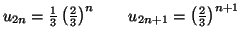
Pour le calcul de 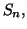 on distingue les cas où
on distingue les cas où 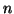 est pair ou bien
impair.
est pair ou bien
impair.
Si 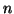 est pair, il peut s'écrire
est pair, il peut s'écrire 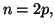 et
et

Si 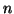 est impair, il
peut s'écrire
est impair, il
peut s'écrire 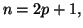 et
et
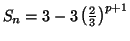
Solution 6.18

Solution 6.20 On obtient les limites suivantes :
On pourra utiliser des factorisations et les résultats sur les croissances
comparées.
Solution 6.19 On obtient les limites suivantes :
Solution 6.21 On a
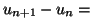
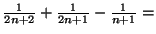
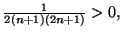 donc la suite
donc la suite
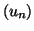 est croissante. De
même,
est croissante. De
même,
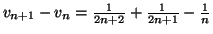 =
=
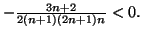
Enfin,
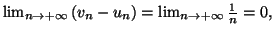 donc ces suites sont adjacentes.
donc ces suites sont adjacentes.
Solution 6.22
- On obtient :
- Comme le point
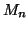 est situé sur le cercle de centre
est situé sur le cercle de centre  et de
rayon
et de
rayon 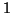 , on peut dire que
D'après la définition de
, on peut dire que
D'après la définition de
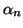 , on peut dire que la suite
, on peut dire que la suite
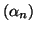 est une suite arithmétique de raison
est une suite arithmétique de raison
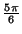 . On en déduit que
Pour tout
. On en déduit que
Pour tout 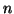 entier naturel, la forme exponentielle de
entier naturel, la forme exponentielle de 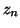 est donc
égale à
est donc
égale à
- a) Remarquons que pour tout entier naturel
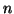 :
ce qui prouve que les points
:
ce qui prouve que les points 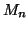 et
et 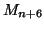 sont diamètralement
opposés.
sont diamètralement
opposés.
De même :
ce qui prouve que les points 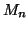 et
et  sont confondus.
sont confondus.
Par
la méthode précédente :
En passant aux modules :
On en déduit alors que
en appliquant la relation précédente à
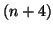 .
Enfin , remarquons que :
ce qui démontre bien que le triangle
.
Enfin , remarquons que :
ce qui démontre bien que le triangle
 est
équilatéral pour tout entier naturel
est
équilatéral pour tout entier naturel 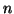 .
.
- Nous sommes dans un cas d'équiprobabilité. Il y a
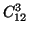 triangles possibles, car on choisit trois cartons parmi 12. Il n'y a que 4
triangles équilatéraux possibles, donc la probabilité de
l'évènement est égale à :
triangles possibles, car on choisit trois cartons parmi 12. Il n'y a que 4
triangles équilatéraux possibles, donc la probabilité de
l'évènement est égale à :
Solution 6.23 On obtient pour tout 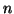 :
:
Si la suite
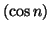 est convergente vers
est convergente vers
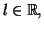 alors on a :
Le système précédent entraîne alors que
alors on a :
Le système précédent entraîne alors que 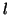 est solution de :
Ce système d'équations n'admet pas de solutions, donc l'hypothèse
de départ est fausse, c'est à dire que la suite
est solution de :
Ce système d'équations n'admet pas de solutions, donc l'hypothèse
de départ est fausse, c'est à dire que la suite
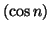 est divergente.
est divergente.
Solution 6.25
- 1.
-
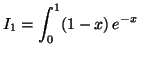 d
d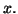
Posons
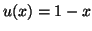 et
et
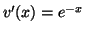 . On déduit
. On déduit
 et
et
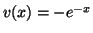 . Les fonctions
. Les fonctions  et
et 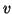 sont dérivables à dérivées dérivables : l'intégration par parties de
sont dérivables à dérivées dérivables : l'intégration par parties de 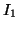 est possible.
est possible.
![$ I_1 = \left[(x_1)e^{-x}\right]_0^1 - \displaystyle \int _0 ^1 e^{-x}$](img1879.gif) d
d![$ x = 1 + \left[e^{-x}\right]_0 ^1$](img1880.gif) . Soit
. Soit
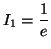
- On a successivement les encadrements :
 donc
donc
 et puisque la fonction puissance
et puisque la fonction puissance 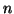 -ème (
-ème (
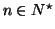 ) est croissante sur
) est croissante sur
![$ \left[0\,,\,1\right]$](img1885.gif) ,
,
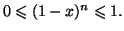
En multipliant les trois membres par le réel strictement positif 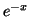 ,
,
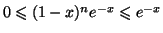 .
.
D'après une propriété de l'intégrale d'une fonction positive sur l'intervalle
![$ \left[0\,,\,1\right]$](img1885.gif) ,
,
Soit en multipiant les trois membres par le réel strictement positif
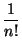 et en reconnaissant
et en reconnaissant 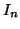 dans le second terme :
dans le second terme :
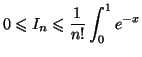 d
d
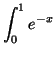 d
d est un réel et la suite de terme général
est un réel et la suite de terme général
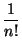 converge vers 0, donc
converge vers 0, donc
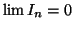
-
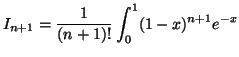 d
d .
.
Posons
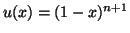 et
et
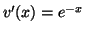 . On déduit
. On déduit
 et
et
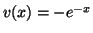 . Les fonctions
. Les fonctions  et
et 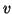 sont dérivables à dérivées dérivables : l'intégration par parties de
sont dérivables à dérivées dérivables : l'intégration par parties de 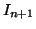 est possible.
est possible.
![$ I_{n+1} = \displaystyle\frac {1}{(n+1)!}\left(\left[-(1-x)^{n+1}e^{-x}\right]_0 ^1 - (n+1)\displaystyle \int _0 ^1 (1-x)^n e^{-x} \mbox{d}x\right)$](img1901.gif) .
.
Soit après simplification
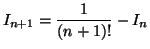
- 2.
 Par hypothèse
Par hypothèse  .
.
En appliquant la formule à démontrer pour 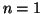 on obtient
on obtient
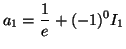 . Or
. Or
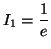 (établi en 1.(a)). Donc
(établi en 1.(a)). Donc  .
La formule est donc vraie pour
.
La formule est donc vraie pour  .
.
 Supposons la formule vraie pour un naturel non nul
Supposons la formule vraie pour un naturel non nul 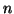 c'est à dire
c'est à dire
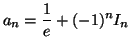 .
.
Il en résulte que
![$ a_{n+1} = \displaystyle\frac {1}{e} + (-1)^n I_n +\displaystyle\frac {(-1)^{n+...
...tyle\frac {1}{e} + (-1)^{n+1} \left[\displaystyle\frac {1}{(n+1)!} - I_n\right]$](img1907.gif) .
.
Soit, d'après le résultat établi en 1.(c),
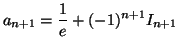 .
La formule, si elle est vraie pour
.
La formule, si elle est vraie pour 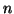 est vraie pour
est vraie pour 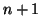 .
.
En conclusion
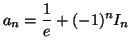 est vraie pour tous les entiers naturels non nuls.
est vraie pour tous les entiers naturels non nuls.
- On déduit du résultat précédent :
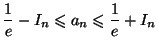 .
.
Or
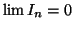 (établi en 1.(b)). Donc
(établi en 1.(b)). Donc
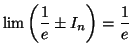 . Soit
. Soit
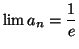
Solution 6.26
Partie A
- Comme
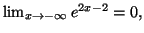 on a
on a
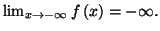
- Il suffit de développer l'expression fournie. D'après le cours
:
donc
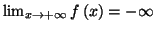 .
.
 est dérivable que
est dérivable que
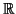 par composition et
différence. On a
Si
par composition et
différence. On a
Si
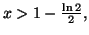 alors
alors
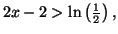 et donc
et donc
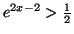 d'après la croissance de la fonction exponentielle.
Cela entraine que
d'après la croissance de la fonction exponentielle.
Cela entraine que
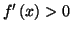 sur
sur
![$ \left] 1-\frac{\ln
2}{2},+\infty\right[ .$](img1923.gif) De même,
De même,
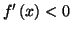 sur
sur
![$ \left] -\infty,1-\frac{\ln2}{2}\right[ $](img1925.gif) . On a
. On a
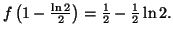
- On démontre que la droite
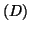 d'équation :
d'équation : 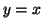 est
asymptote à la courbe
est
asymptote à la courbe 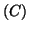 en remarquant que :
Comme
en remarquant que :
Comme
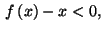 on peut dire que
on peut dire que 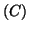 est située
au-dessous de
est située
au-dessous de 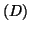 .
.
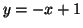 .
.
 est inclus dans
est inclus dans
![$ \left] -\infty,1-\frac{\ln2}{2}\right[ ,$](img1930.gif) donc la
fonction
donc la
fonction  est strictement décroissante sur
est strictement décroissante sur 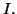 De plus, elle est
dérivable et
De plus, elle est
dérivable et

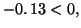 tandis que
tandis que
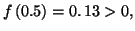 ce qui prouve bien que l'équation :
ce qui prouve bien que l'équation : 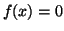 admet
dans l'intervalle
admet
dans l'intervalle 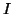 une unique solution appelée
une unique solution appelée  .
.
- Par dichotomie, on a
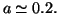
Partie B
-
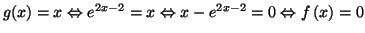 . On a donc
. On a donc
 puisque
puisque
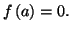
-
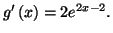 On a alors :
car la fonction exponentielle est croissante. On en déduit facilement que
ce qui prouve bien que pour tout réel
On a alors :
car la fonction exponentielle est croissante. On en déduit facilement que
ce qui prouve bien que pour tout réel  de l'intervalle
de l'intervalle 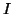 on a :
on a :
-
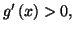 donc
donc 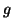 est une fonction strictement
croissante sur
est une fonction strictement
croissante sur
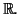 En conséquence, l'image de
En conséquence, l'image de 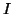 par
par 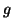 est
égal à
est
égal à
![$ \left[ g\left( 0\right) ,g\left( 0.5\right) \right] $](img1943.gif) .
Or
.
Or
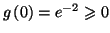 et
et
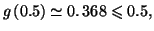 donc
donc
 est bien inclus dans
est bien inclus dans 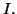
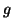 est dérivable sur
est dérivable sur 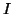 et pour tout
et pour tout  de
de 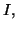 on a
on a
 donc pour tout
donc pour tout  et
et 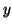 de
de 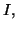 on a
Montrons maintenant par récurrence sur
on a
Montrons maintenant par récurrence sur 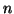 que pour tout
que pour tout 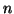 de
de

 appartient à
appartient à 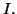
- Soit
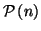 l'hypothèse de récurrence
à l'ordre
l'hypothèse de récurrence
à l'ordre 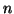 :
:
- On a
donc le théorème des gendarmes prouve que la suite
 converge
vers
converge
vers 
- L'inégalité
 est vérifiée dès
que
est vérifiée dès
que
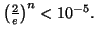 On en déduit :
Comme
on peut donc affirmer que l'entier
On en déduit :
Comme
on peut donc affirmer que l'entier 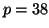 convient.
convient.
- On définit la fonction
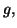 puis on calcule
puis on calcule
 , ce qui donne
, ce qui donne 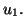 On réitère le
procédé en remplaçant
On réitère le
procédé en remplaçant 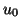 par
par 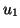 et
et 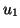 par
par 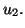 On calcule de cette manière
On calcule de cette manière 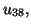 qui fournit d'après la question
précédente une valeur approchée de
qui fournit d'après la question
précédente une valeur approchée de  à
à 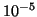 près.
près.




suivant: Séries numériques
monter: Suites numériques
précédent: Exercices
Table des matières
Michel
2002-08-06
![\begin{displaymath}
\begin{array}[c]{lllll}
u_{2}=1 & u_{3}=\frac{5}{8} & u_{4}=...
...ak\ln\frac{3}{2} & w_{10}=\allowbreak\ln\frac{7}{5}
\end{array}\end{displaymath}](img1799.gif)
![\begin{displaymath}
\begin{array}[c]{lllll}
u_{2}=1 & u_{3}=\frac{5}{8} & u_{4}=...
...ak\ln\frac{3}{2} & w_{10}=\allowbreak\ln\frac{7}{5}
\end{array}\end{displaymath}](img1799.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![$\displaystyle \begin{tabular}[c]{ll}
INPUT $N$\ & Entr\'{e}e de la valeur de $n...
...e\\
End & Fin de la boucle\\
PRINT $S$\ & Affichage de la somme
\end{tabular}$](img1809.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() c) On trouve que
c) On trouve que ![]()
![]()
![]()
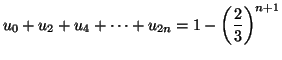
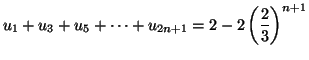
![]()
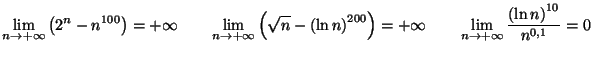
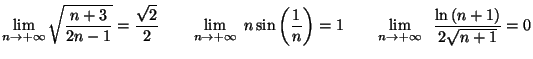
![]()
![]()
![]() donc la suite
donc la suite
![]() est croissante. De
même,
est croissante. De
même,
![]() =
=
![]()
![]() donc ces suites sont adjacentes.
donc ces suites sont adjacentes.
![\includegraphics[]{d1s-f2}](img1854.gif)
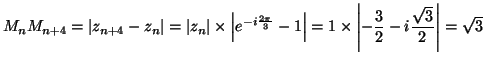
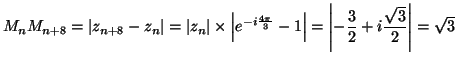
![]() :
:
![\begin{displaymath}
\left\{
\begin{array}[c]{l}
\cos\left( n+2\right) +\cos n=\f...
...ight)
+\cos1\right) \\
\cos2n=2\cos^{2}n-1
\end{array}\right.
\end{displaymath}](img1869.gif)
![\begin{displaymath}
\left\{
\begin{array}[c]{l}
2l=\frac{1}{2}\left( l+\cos1\right) \\
l=2l^{2}-1
\end{array}\right.
\end{displaymath}](img1872.gif)
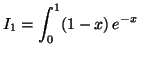 d
d![$ I_1 = \left[(x_1)e^{-x}\right]_0^1 - \displaystyle \int _0 ^1 e^{-x}$](img1879.gif) d
d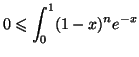 d
d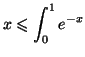 d
d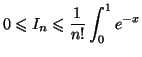 d
d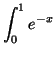 d
d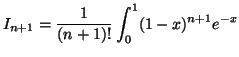 d
d![$ I_{n+1} = \displaystyle\frac {1}{(n+1)!}\left(\left[-(1-x)^{n+1}e^{-x}\right]_0 ^1 - (n+1)\displaystyle \int _0 ^1 (1-x)^n e^{-x} \mbox{d}x\right)$](img1901.gif) .
.
![$ a_{n+1} = \displaystyle\frac {1}{e} + (-1)^n I_n +\displaystyle\frac {(-1)^{n+...
...tyle\frac {1}{e} + (-1)^{n+1} \left[\displaystyle\frac {1}{(n+1)!} - I_n\right]$](img1907.gif) .
.
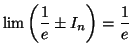 . Soit
. Soit
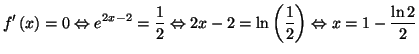
![\includegraphics[]{capes20.eps}](img1935.gif)
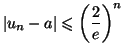
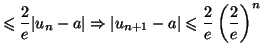 d'après question 4
d'après question 4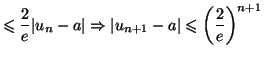 d'après
d'après