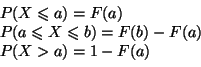


suivant: Espérance mathématique, variance, écart-type
monter: Autres exemples
précédent: Exemple de variable aléatoire
Table des matières
Exemple de variable aléatoire continue

On peut être amené à étudier des variables aléatoires pouvant prendre,
au moins théoriquement, n'importe quelle valeur dans
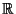 ou un intervalle de
ou un intervalle de
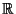 . Par exemple, considérons la variable
aléatoire
. Par exemple, considérons la variable
aléatoire  mesurant la durée de bon fonctionnement, en jours,
d'un équipement particulier fabriqué en grande série, avec l'intervalle
mesurant la durée de bon fonctionnement, en jours,
d'un équipement particulier fabriqué en grande série, avec l'intervalle
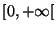 . Pour une telle variable, les évènements
intéressants sont par exemple
. Pour une telle variable, les évènements
intéressants sont par exemple
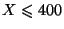 , ou
, ou
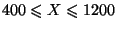 .
Dans ce cas, la fonction de répartition joue un rôle fondamental et
permet de calculer des probabilités. On suppose que cette fonction
de répartition
.
Dans ce cas, la fonction de répartition joue un rôle fondamental et
permet de calculer des probabilités. On suppose que cette fonction
de répartition 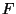 est définie par :
est définie par :
où pour tout
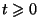 :
Ainsi, pour tout
:
Ainsi, pour tout 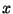 positif,
positif, 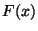 est l'aire de la portion de
plan en grisé sur la figure ci-dessous :
est l'aire de la portion de
plan en grisé sur la figure ci-dessous :
On en déduit que
En utilisant l'évènement contraire de 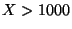 , nous obtenons que
Pour calculer
remarquons que
car les deux évènements
, nous obtenons que
Pour calculer
remarquons que
car les deux évènements
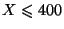 et
et
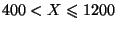 sont incompatibles. On en déduit alors :
sont incompatibles. On en déduit alors :
Nous admettrons que
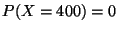 et de manière générale, que pour
tout
et de manière générale, que pour
tout
 ,
, 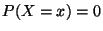 . En conclusion, pour tout
. En conclusion, pour tout 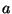 et
et
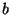 tels que
tels que
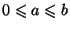 ,
,
Définition 5
La fonction
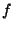
définie pour tout
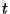
positif par
est la densité de probabilité de la variable aléatoire

.
C'est une fonction telle que pour tout 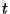 positif, on ait
positif, on ait
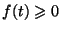 .
D'autre part, nous avons vu que pour tout
.
D'autre part, nous avons vu que pour tout
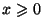 :
donc
On convient d'écrire ce résultat
Comme la fonction
:
donc
On convient d'écrire ce résultat
Comme la fonction 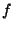 est nulle sur
est nulle sur
![$ \left]-\infty ,0\right]$](img80.gif) , on
écrit :
Pour la même raison, nous pouvons écrire que pour tout
, on
écrit :
Pour la même raison, nous pouvons écrire que pour tout 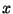 réel
réel
Définition 6
La variable aléatoire

est dite continue s'il existe une fonction
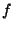
positive et continue sur
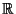
, appelée densité de probabilité
de

, telle que
Définition 7
On appelle fonction de répartition de la variable aléatoire

la
fonction
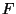
définie sur
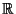
par
On peut remarquer que cette fonction de répartition est une primitive
de 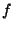 , ce qui pemet d'écrire la proposition
, ce qui pemet d'écrire la proposition ![[*]](crossref.png) sous la forme suivante :
sous la forme suivante :



suivant: Espérance mathématique, variance, écart-type
monter: Autres exemples
précédent: Exemple de variable aléatoire
Table des matières
Michel
2002-07-27
![]()
![]() ou un intervalle de
ou un intervalle de
![]() . Par exemple, considérons la variable
aléatoire
. Par exemple, considérons la variable
aléatoire ![]() mesurant la durée de bon fonctionnement, en jours,
d'un équipement particulier fabriqué en grande série, avec l'intervalle
mesurant la durée de bon fonctionnement, en jours,
d'un équipement particulier fabriqué en grande série, avec l'intervalle
![]() . Pour une telle variable, les évènements
intéressants sont par exemple
. Pour une telle variable, les évènements
intéressants sont par exemple
![]() , ou
, ou
![]() .
Dans ce cas, la fonction de répartition joue un rôle fondamental et
permet de calculer des probabilités. On suppose que cette fonction
de répartition
.
Dans ce cas, la fonction de répartition joue un rôle fondamental et
permet de calculer des probabilités. On suppose que cette fonction
de répartition ![]() est définie par :
est définie par :
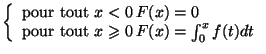
![\includegraphics[ scale=0.8]{varf1}](img58.gif)
![\includegraphics[ scale=0.8]{varf2}](img66.gif)
![]() et de manière générale, que pour
tout
et de manière générale, que pour
tout
![]() ,
, ![]() . En conclusion, pour tout
. En conclusion, pour tout ![]() et
et
![]() tels que
tels que
![]() ,
,
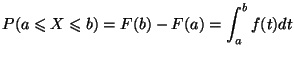
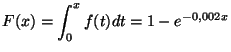
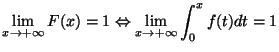
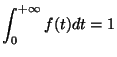
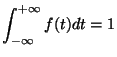
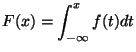
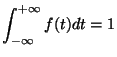
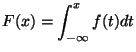
![[*]](crossref.png) sous la forme suivante :
sous la forme suivante :