![]()
Considérons une population d'effectif ![]() , de moyenne
, de moyenne ![]() et d'écart-type
et d'écart-type
![]() . Prélevons, dans cette population, un échantillon de taille
. Prélevons, dans cette population, un échantillon de taille
![]() . On note
. On note
![]() la moyenne de cet échantillon et
la moyenne de cet échantillon et ![]() son écart-type. Considérons les
son écart-type. Considérons les ![]() variables aléatoires
variables aléatoires ![]() ,
,
![]() , ...,
, ..., ![]() où chaque variable aléatoire
où chaque variable aléatoire ![]() associe
au
associe
au ![]() -ième tirage le nombre correspondant à l'élément choisi. Si
nous supposons que le tirage des
-ième tirage le nombre correspondant à l'élément choisi. Si
nous supposons que le tirage des ![]() éléments de l'échantillon a
été effectué avec remise, alors la variables aléatoires
éléments de l'échantillon a
été effectué avec remise, alors la variables aléatoires ![]() sont
indépendantes. Elles suivent toutes la même loi, ont toutes la même
moyenne
sont
indépendantes. Elles suivent toutes la même loi, ont toutes la même
moyenne ![]() et le même écart-type
et le même écart-type ![]() . La variable aléatoire
. La variable aléatoire
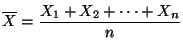
![[*]](crossref.png) de
la limite centrée, pour
de
la limite centrée, pour