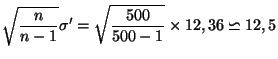Proposition 9
On choisit le nombre
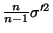
, où
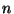
est l'effectif
de l'échantillon et
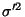
la variance d'un échantillon prélevé
au hasard dans une population, comme estimation ponctuelle de la variance
inconnue
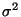
de cette population.
Proposition 10
On choisit le nombre
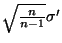
, où
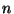
est
l'effectif de l'échantillon et
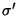
l'écart-type d'un échantillon
prélevé au hasard dans une population, comme estimation ponctuelle
de l'écart-type inconnu
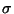
de cette population.
Exemple 5
On se place dans la situation de l'exemple
![[*]](crossref.png)
précédent, et l'on suppose que l'écart-type de l'échantillon des 36
pièces est égal à 12,36. Une estimation ponctuelle de l'écart-type
des 500 pièces est donc égale à
![[*]](crossref.png) précédent, et l'on suppose que l'écart-type de l'échantillon des 36
pièces est égal à 12,36. Une estimation ponctuelle de l'écart-type
des 500 pièces est donc égale à
précédent, et l'on suppose que l'écart-type de l'échantillon des 36
pièces est égal à 12,36. Une estimation ponctuelle de l'écart-type
des 500 pièces est donc égale à