

suivant: Correction des exercices
monter: Estimation par intervalle de
précédent: Moyenne
Table des matières

Soit 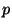 la fréquence inconnue des éléments de la population qui
vérifient une certaine propriété. Soit
la fréquence inconnue des éléments de la population qui
vérifient une certaine propriété. Soit 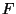 la variable aléatoire
qui, à chacun des échantillons prélevés associe la fréquence des éléments
de cet échantillon vérifiant une certaine propriété.
la variable aléatoire
qui, à chacun des échantillons prélevés associe la fréquence des éléments
de cet échantillon vérifiant une certaine propriété. 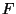 prend successivement
les valeurs
prend successivement
les valeurs 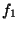 ,
, 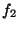 , etc... La variable aléatoire
, etc... La variable aléatoire 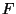 peut être considérée comme suivant la loi normale
peut être considérée comme suivant la loi normale
En effectuant des calculs analogues à ceux du paragraphe précédent,
on obtient :
Or, la constante inconnue 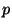 figure aussi dans
figure aussi dans
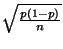 ,
écart-type de
,
écart-type de 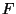 , qui intervient dans l'encadrement de
, qui intervient dans l'encadrement de 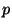 . Pour
. Pour
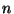 sufffisamment grand, on peut remplacer dans l'expression
sufffisamment grand, on peut remplacer dans l'expression
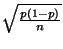 l'inconnue
l'inconnue 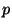 par son estimation ponctuelle
par son estimation ponctuelle 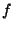 . D'autre part,
puisque
. D'autre part,
puisque
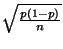 est un écart-type, on doit multiplier
par
est un écart-type, on doit multiplier
par
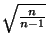 l'estimation ponctuelle
l'estimation ponctuelle
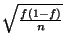 d'après le cours précédent, et donc on obtient
d'après le cours précédent, et donc on obtient
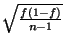 .
En conséquence, on peut énoncer la proposition suivante :
.
En conséquence, on peut énoncer la proposition suivante :
Proposition 11
L'intervalle
est l'intervalle de confiance d'une fréquence
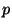
de la population
avec le coefficient de confiance
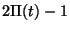
, ayant pour centre
la fréquence analogue
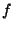
de l'échantillon considéré.
Il existe deux cas particuliers usuels :
- pour le coefficient de confiance 95%,
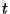 vaut 1,96
vaut 1,96
- pour le coefficient de confiance 99%,
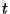 vaut 2,58.
vaut 2,58.
Dans le cas où 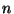 n'est pas petit par rapport à l'effectif
n'est pas petit par rapport à l'effectif 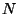 de la population et où le tirage des éléments d'un échantillon est
sans remise, alors l'écart-type de
de la population et où le tirage des éléments d'un échantillon est
sans remise, alors l'écart-type de 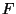 est :
est :
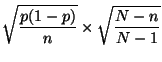
Une entreprise de matériel pour l'industrie produit des modules
constitués de deux types de pièces : 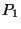 et
et 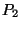 .
.
- Une pièce
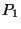 est considérée comme bonne si sa
longueur, en centimètres, est comprise entre
est considérée comme bonne si sa
longueur, en centimètres, est comprise entre 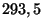 et
et 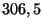 .
On note
.
On note 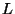 la variable aléatoire qui, à chaque pièce
la variable aléatoire qui, à chaque pièce
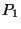 choisie au hasard dans la production d'une journée,
associe sa longueur. On suppose que
choisie au hasard dans la production d'une journée,
associe sa longueur. On suppose que 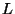 suit une loi normale de moyenne
suit une loi normale de moyenne
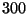 et d'écart type
et d'écart type 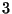 .
.
Déterminer, à 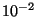 près, la probabilité
qu'une pièce
près, la probabilité
qu'une pièce 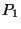 soit bonne.
soit bonne.
- On note
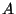 l'événement : '' une pièce
l'événement : '' une pièce 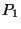 choisie au hasard dans la production des pièces
choisie au hasard dans la production des pièces 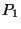 est
défectueuse '' On note de même
est
défectueuse '' On note de même 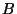 l'événement :
'' une pièce
l'événement :
'' une pièce 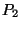 choisie au hasard dans la production des
pièces
choisie au hasard dans la production des
pièces 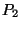 est défectueuse ''.
est défectueuse ''.
On admet que les probabilités des deux événements 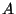 et
et 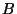 sont
sont 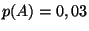 et
et 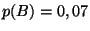 et on suppose que ces deux
événements sont indépendants.
et on suppose que ces deux
événements sont indépendants.
Un module étant choisi au hasard dans la production, calculer,
à 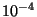 près, la probabilité de chacun des événements
suivants :
près, la probabilité de chacun des événements
suivants :
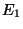 : '' les deux pièces du module sont défectueuses.
''
: '' les deux pièces du module sont défectueuses.
''
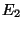 : '' au moins une des deux pièces du module est défectueuse.
''
: '' au moins une des deux pièces du module est défectueuse.
''
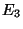 : '' aucune des deux pièces constituant le module
n'est défectueuse. ''
: '' aucune des deux pièces constituant le module
n'est défectueuse. ''
- Dans un important stock de ces modules, on prélève au hasard
10 modules pour vérification. Le stock est assez important pour
qu'on puisse assimiler ce prélèvement à un tirage avec
remise de
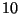 modules.
modules.
On considère la variable aléatoire  qui, à tout
prélèvement de
qui, à tout
prélèvement de 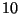 modules associe le nombre de modules
réalisant l'événement
modules associe le nombre de modules
réalisant l'événement 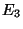 défini au 2.
On suppose que la probabilité de l'événement
défini au 2.
On suppose que la probabilité de l'événement 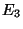 est
est 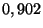 .
.
- Expliquer pourquoi
 suit une loi binômiale ; déterminer
les paramètres de cette loi.
suit une loi binômiale ; déterminer
les paramètres de cette loi.
- Calculer, à
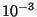 près, la probabilité que, dans
un tel prélèvement,
près, la probabilité que, dans
un tel prélèvement, 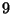 modules au moins réalisent
l'événement
modules au moins réalisent
l'événement 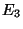 .
.
- Dans cette question on s'intéresse au diamètre des pièces
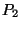 .
.
Soit
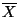 la variable aléatoire qui, à tout échantillon
de
la variable aléatoire qui, à tout échantillon
de 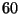 pièces
pièces 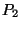 prélevées au hasard et avec
remise dans la production de la journée considérée,
associe la moyenne des diamètres des pièces de cet échantillon.
On suppose que
prélevées au hasard et avec
remise dans la production de la journée considérée,
associe la moyenne des diamètres des pièces de cet échantillon.
On suppose que
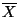 suit la loi normale de moyenne inconnue
suit la loi normale de moyenne inconnue
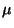 et d'écart-type
et d'écart-type
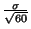 avec
avec
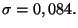
On mesure le diamètre, exprimé en centimètres, de chacune
des 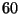 pièces
pièces 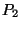 d'un échantillon choisi au hasard
et avec remise dans la production d'une journée.
d'un échantillon choisi au hasard
et avec remise dans la production d'une journée.
On constate que la valeur approchée arrondie à 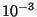 près
de la moyenne
près
de la moyenne
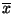 de cet échantillon est
de cet échantillon est
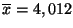 .
.
- À partir des informations portant sur cet échantillon, donner
une estimation ponctuelle, à
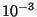 près, de la moyenne
près, de la moyenne
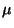 des diamètres des pièces
des diamètres des pièces 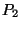 produites pendant
cette journée.
produites pendant
cette journée.
- Déterminer un intervalle de confiance centré en
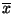 de la moyenne
de la moyenne 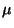 des diamètres des pièces
des diamètres des pièces 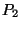 produites pendant la journée considérée, avec le coefficient
de confiance de
produites pendant la journée considérée, avec le coefficient
de confiance de 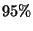 .
.
- On considère l'affirmation suivante : " la moyenne
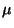 est obligatoirement entre
est obligatoirement entre 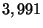 et
et 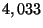 ".
Peut-on déduire de ce qui précède qu'elle est vraie ?
".
Peut-on déduire de ce qui précède qu'elle est vraie ?
Les quatre questions de cet exercice sont indépendantes.
Dans un groupe d'assurances, on s'intéresse aux sinistres susceptibles
de survenir, une année donnée, aux véhicules de la
flotte d'une importante entreprise de maintenance de chauffage collectif.
Dans cet exercice, sauf mention contraire, les résultats approchés
sont à arrondir à 10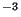 .
.
- Etude du nombre de sinistres par véhicule
Soit  la variable aléatoire qui, à tout véhicule
tiré au hasard dans un des parcs de la flotte, associe le nombre
de sinistres survenant pendant l'année considérée.
On admet que
la variable aléatoire qui, à tout véhicule
tiré au hasard dans un des parcs de la flotte, associe le nombre
de sinistres survenant pendant l'année considérée.
On admet que  suit la loi de Poisson de paramètre 0,28.
suit la loi de Poisson de paramètre 0,28.
- Calculer la probabilité de l'évènement A : '' un véhicule
tiré au hasard dans le parc n'a aucun sinistre pendant l'année
considérée ''
- Calculer la probabilité de l'évènement B : '' un véhicule
tiré au hasard dans le parc a, au plus, deux sinistres pendant
l'année considérée ''
- Etude du nombre de sinistres dans une équipe de 15 conducteurs.
On note E l'évènement : '' un conducteur tiré au hasard
dans l'ensemble des conducteurs de l'entreprise n'a pas de sinistre
pendant l'année considérée. On suppose que la probabilité
de l'évènement E est 0,6.
On tire au hasard 15 conducteurs dans l'effectif des conducteurs de
l'entreprise. Cet effectif est assez important pour que l'on puisse
assimiler ce prélèvement à un tirage avec remise de
15 conducteurs.
On considère la variable aléatoire 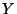 qui, à tout
prélèvement de 15 conducteurs, associe le nombre de conducteurs
n'ayant pas de sinistre pendant l'année considérée.
qui, à tout
prélèvement de 15 conducteurs, associe le nombre de conducteurs
n'ayant pas de sinistre pendant l'année considérée.
- Justifier que la variable aléatoire
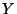 suite une loi binomiale
et déterminer ses paramètres.
suite une loi binomiale
et déterminer ses paramètres.
- Caculer la probabilité que, dans un tel prélèvement,
10 conducteurs n'aient pas de sinistre pendant l'année considérée.
- Etude du coût des sinistres
Dans ce qui suit, on s'intéresse au coût d'une certaine
catégorie de sinistres survenus dans l'entreprise pendant l'année
considérée.
On considère la variable aléatoire 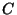 qui, à chaque
sinistre tiré au hasard parmi les sinistres de cette catégorie,
associe son coût en euros. On suppose que
qui, à chaque
sinistre tiré au hasard parmi les sinistres de cette catégorie,
associe son coût en euros. On suppose que 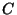 suit la loi normale
de moyenne 1200 et d'écart type 200.
suit la loi normale
de moyenne 1200 et d'écart type 200.
Calculer la probabilité qu'un sinistre tiré au hasard parmi
les sinistres de ce type coûte entre 1000 euros et 1500 euros.
- On considère un échantillon de 100 véhicules prélevés
au hasard dans le parc de véhicules mis en service depuis 6 mois.
Ce parc contient suffisamment de véhicules pour qu'on puisse
assimiler ce tirage à un tirage avec remise. On constate que
91 véhicules de cet échantillon n'ont pas eu de sinistre.
- Donner une estimation ponctuelle du pourcentage
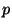 de véhicules
de ce parc qui n'ont pas eu de sinistre 6 mois après leur mise
en service.
de véhicules
de ce parc qui n'ont pas eu de sinistre 6 mois après leur mise
en service.
- Soit
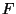 la variable aléatoire qui à tout échantillon
de 100 véhicules prélevés au hasard et avec remise
dans ce parc, associe le pourcentage de véhicules qui n'ont pas
eu de sinistre 6 mois après leur mise en service.
la variable aléatoire qui à tout échantillon
de 100 véhicules prélevés au hasard et avec remise
dans ce parc, associe le pourcentage de véhicules qui n'ont pas
eu de sinistre 6 mois après leur mise en service.
On suppose que 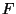 suit la loi normale
où
suit la loi normale
où 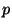 est le pourcentage inconnu de véhicules du parc
qui n'ont pas eu de sinistre 6 mois après leur mise en service.
est le pourcentage inconnu de véhicules du parc
qui n'ont pas eu de sinistre 6 mois après leur mise en service.
Déterminer un intervalle de confiance du pourcentage 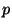 avec
le coefficient de confiance 95%.
avec
le coefficient de confiance 95%.
- On considère l'affirmation suivante :
'' le pourcentage 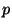 est obligatoirement dans l'intervalle de confiance
obtenu à la question b) ''
est obligatoirement dans l'intervalle de confiance
obtenu à la question b) ''
Est-elle vraie ? On ne demande pas de justification.

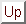


suivant: Correction des exercices
monter: Estimation par intervalle de
précédent: Moyenne
Table des matières
Michel
2002-07-27
![]()
![]() la fréquence inconnue des éléments de la population qui
vérifient une certaine propriété. Soit
la fréquence inconnue des éléments de la population qui
vérifient une certaine propriété. Soit ![]() la variable aléatoire
qui, à chacun des échantillons prélevés associe la fréquence des éléments
de cet échantillon vérifiant une certaine propriété.
la variable aléatoire
qui, à chacun des échantillons prélevés associe la fréquence des éléments
de cet échantillon vérifiant une certaine propriété. ![]() prend successivement
les valeurs
prend successivement
les valeurs ![]() ,
, ![]() , etc... La variable aléatoire
, etc... La variable aléatoire ![]() peut être considérée comme suivant la loi normale
peut être considérée comme suivant la loi normale
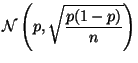
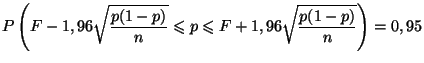
![$\displaystyle \left[f-t\sqrt{\frac{f(1-f)}{n}};f+t\sqrt{\frac{f(1-f)}{n}}\right]$](img304.gif)
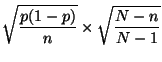
![]() .
.