![]()
Dans la situation de l'exemple ![[*]](crossref.png) ,
plutôt que d'estimer à 774,7 grammes la moyenne inconnue
,
plutôt que d'estimer à 774,7 grammes la moyenne inconnue ![]() des
masses des 500 pièces, nous allons mettre en oeuvre une méthode permettant
d'obtenir des intervalles qui, dans un grand pourcentage de cas choisi
à l'avance, par exemple 95% ou 99%, contiennent la moyenne inconnue
des
masses des 500 pièces, nous allons mettre en oeuvre une méthode permettant
d'obtenir des intervalles qui, dans un grand pourcentage de cas choisi
à l'avance, par exemple 95% ou 99%, contiennent la moyenne inconnue
![]() de la population.
de la population.
Imaginons, que dans la population des 500 pièces, on prélève au hasard
et avec remise une succession d'échantillons de même effectif ![]() dont on calcule les moyennes respectives
dont on calcule les moyennes respectives
![]() pour
le premier échantillon,
pour
le premier échantillon,
![]() pour le deuxième échantillon,
et ainsi de suite. De plus, on suppose que l'écart-type
pour le deuxième échantillon,
et ainsi de suite. De plus, on suppose que l'écart-type ![]() de cette population est connu et égal à 12,5 grammes. Soit
de cette population est connu et égal à 12,5 grammes. Soit
![]() la variable aléatoire qui, à chacun de ces échantillons de taille
36 associe la moyenne de cet échantillon.
la variable aléatoire qui, à chacun de ces échantillons de taille
36 associe la moyenne de cet échantillon.
![]() prend successivement
les valeurs
prend successivement
les valeurs
![]() ,
,
![]() , ...
, ...
On suppose que les conditions sont réunies pour pouvoir utiliser une
conséquence du théorème ![[*]](crossref.png) de la limité centrée
et faire l'approximation que la variable aléatoire
de la limité centrée
et faire l'approximation que la variable aléatoire
![]() suit la loi normale
suit la loi normale
![]() . Dans ce cas, la variable aléatoire
. Dans ce cas, la variable aléatoire
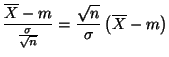
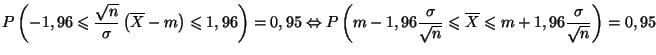
![$\displaystyle \left[m-1,96\frac{\sigma }{\sqrt{n}};m+1,96\frac{\sigma }{\sqrt{n}}\right]$](img284.gif)
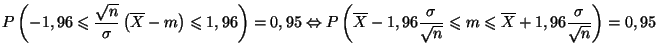
En revanche, après le prélèvement d'un échantillon, il n'y a plus
de probabilités à envisager. Il est vrai ou faux de dire que la moyenne
![]() de la population est située dans l'intervalle fixe
de la population est située dans l'intervalle fixe
![$\displaystyle \left[\overline{x}-1,96\frac{\sigma }{\sqrt{n}};\overline{x}+1,96\frac{\sigma }{\sqrt{n}}\right]$](img288.gif)
Dans le cas de l'exemple ![[*]](crossref.png) ,
on a
,
on a ![]() ,
,
![]() et
et
![]() donc
donc
![$\displaystyle \left[\overline{x}-1,96\frac{\sigma }{\sqrt{n}};\overline{x}+1,96\frac{\sigma }{\sqrt{n}}\right]=\left[770,61;778,79\right]$](img291.gif)
Si on prélevait un très grand nombre de tels échantillons, environ
95 pour 100 d'entre eux contiendraient la moyenne inconnue ![]() de
la population. En fait, on n'en prélève qu'un seul, et on ne peut
pas savoir si celui-ci contient ou non le nombre
de
la population. En fait, on n'en prélève qu'un seul, et on ne peut
pas savoir si celui-ci contient ou non le nombre ![]() , mais la méthode
mise en oeuvre permet d'obtenir un intervalle contenant
, mais la méthode
mise en oeuvre permet d'obtenir un intervalle contenant ![]() dans
95 cas sur 100.
dans
95 cas sur 100.
De manière générale, on peut donc énoncer :
![$\displaystyle \left[\overline{x}-t\frac{\sigma }{\sqrt{n}};\overline{x}+t\frac{\sigma }{\sqrt{n}}\right]$](img292.gif)
Dans le cas où ![]() n'est pas petit par rapport à l'effectif
n'est pas petit par rapport à l'effectif ![]() de la population et où le tirage des éléments d'un échantillon se
fait sans remise, l'écart-type de
de la population et où le tirage des éléments d'un échantillon se
fait sans remise, l'écart-type de
![]() est
est
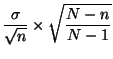
On ne peut pas savoir si la moyenne ![]() de la population appartient
ou non à l'intervalle de confiance associé au seul échantillon prélevé.
D'autre part, si
de la population appartient
ou non à l'intervalle de confiance associé au seul échantillon prélevé.
D'autre part, si ![]() appartient à cet intervalle,
appartient à cet intervalle, ![]() n'a pas plus
de raison d'être près du centre
n'a pas plus
de raison d'être près du centre
![]() de l'intervalle que
près d'une de ses extrémités ou en tout autre endroit de l'intervalle.
de l'intervalle que
près d'une de ses extrémités ou en tout autre endroit de l'intervalle.