


suivant: Loi de probabilité ou
monter: Exemple
précédent: Variable aléatoire à valeurs
Table des matières

Un joueur préfère maintenant, avant de jouer, connaître la probabilité
de gagner 12 euros plutôt que celle de tirer une boule de telle couleur.
On va donc construire, à partir de la probabilité 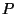 définie sur
définie sur
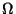 , une nouvelle probabilité
, une nouvelle probabilité 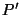 définie sur
définie sur
Pour toute partie 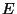 de
de
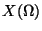 , on veut définir une probabilité
, on veut définir une probabilité
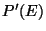 à l'aide de
à l'aide de 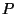 et de
et de  . Par exemple, le singleton
. Par exemple, le singleton
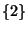 de
de
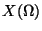 est l'image par
est l'image par  de la partie
de la partie
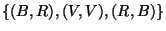 de
de 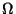 . Comme
on est conduit à poser
. Comme
on est conduit à poser
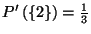 .
De même, l'évènement
.
De même, l'évènement 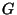 ``avoir un gain positif `` est l'image
par
``avoir un gain positif `` est l'image
par  de la partie
et donc on a
de la partie
et donc on a
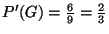 .
.
D'une manière générale, soit 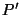 l'application qui, à toute partie
l'application qui, à toute partie
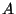 de
de
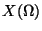 associe le nombre
associe le nombre
On peut démontrer que 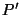 vérifie les axiomes d'une probabilité
définie sur
vérifie les axiomes d'une probabilité
définie sur
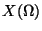 , c'est à dire que
, c'est à dire que
-
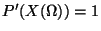
- Pour toutes parties
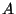 et
et 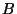 de
de
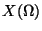 disjointes, on a
disjointes, on a
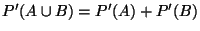 .
.
Définition 2
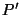
est la probabilité image de la probabilité
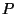
par la variable
aléatoire

.
On conviendra d'utiliser la notation suivante :
D'une manière générale, pour tout nombre 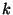 de
de
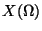 , on
note
, on
note 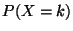 le nombre
le nombre

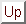


suivant: Loi de probabilité ou
monter: Exemple
précédent: Variable aléatoire à valeurs
Table des matières
Michel
2002-07-27
![]()
![]() définie sur
définie sur
![]() , une nouvelle probabilité
, une nouvelle probabilité ![]() définie sur
définie sur
![]() l'application qui, à toute partie
l'application qui, à toute partie
![]() de
de
![]() associe le nombre
associe le nombre
![]() de
de
![]() , on
note
, on
note ![]() le nombre
le nombre